B . 
C . 
D . 
B . 
C . 
D . 
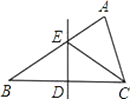
已知：如图，在Rt△ABC中，∠ABC＝90°，
求作：点D ， 使点D在BC边上，且到AB和AC的距离相等．
作法：①如图，以点A为圆心，任意长为半径画弧， 分别交AB，AC于点M、N；
②分别以点M ， N为圆心，大于 MN的长为半径画弧， 两弧交于点P；
③画射线AP ， 交BC于点D ．
所以点D即为所求．
根据小东设计的尺规作图过程：
证明：过点D作DE⊥AC于点E ， 连接MP ， NP ．
在△AMP与△ANP中，
∵AM＝AN ， MP＝NP ， AP＝AP ，
∴△AMP≌△ANP（SSS）．
∴∠ ▲ ＝∠ ▲ ．
∵∠ABC＝90°，
∴DB⊥AB ．
又∵DE⊥AC ，
∴DB＝DE（ ▲ ）（填推理的依据）
例如：分解因式：x2+2x﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；
又例如：求代数式2x2+4x﹣6的最小值：∵2x2+4x﹣6＝2（x2+2x﹣3）＝2（x+1）2﹣8；
又∵（x+1）2≥0；当x＝﹣1时，2x2+4x﹣6有最小值，最小值是﹣8．
根据阅读材料，利用“配方法”，解决下列问题：
