河北省张家口市桥西区2023-2024学年九年级上学期期中数...

更新时间：2024-01-30 浏览次数：37 类型：期中考试

一、选择题（本大题共16个小题，共38分．1～6小题各3分，7～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2023九上·桥西期中) 下列函数中，是二次函数的是（　　）

A . y＝2x﹣1 B . y＝2x²﹣1 C . 2x²＝1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·博山期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 6 B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 下列是描述小明和小颖在同一盏路灯下影子的图片，其中合理的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 若两个相似三角形周长的比为 $\text{[math]}$ ，则这两个三角形对应边的比是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·桥西期中) 反比例函数 $\text{[math]}$ 的图象一定不经过的点是（　　）

A . （﹣3，﹣2） B . （2，3） C . （2，﹣3） D . （﹣2，﹣4）

答案解析收藏纠错 + 选题
6. (2023九上·桥西期中) 在△ABC中，∠A、∠B、∠C的对边分别为a、b、c ．已知a＝5，b＝12，c＝13，则tan∠A的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·桥西期中) 如图的立体图形由相同大小的正方体积木堆叠而成．判断拿走图中的哪一个积木后，此图形前视图的形状会改变（　　）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
8. (2023九上·桥西期中) 一元二次方程x²+5＝4x根的情况为（　　）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 不能判定

答案解析收藏纠错 + 选题
9. (2023九上·桥西期中) 如图，四边形ABCD是菱形，对角线AC与BD相交于点O ， AB＝5，AO＝4，则BD等于（　　）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
10. (2023九上·桥西期中) 用配方法解方程x²﹣4x﹣1＝0时，配方后正确的是（　　）

A . （x+2）²＝3 B . （x+2）²＝17 C . （x﹣2）²＝5 D . （x﹣2）²＝17

答案解析收藏纠错 + 选题
11. 如图，将四根木条用钉子钉成一个矩形框架 $\text{[math]}$ ，然后向左扭动框架，观察所得四边形的变化．下面判断错误的是（）

A . 四边形 $\text{[math]}$ 由矩形变为平行四边形 B . 对角线 $\text{[math]}$ 的长度减小 C . 四边形 $\text{[math]}$ 的面积不变 D . 四边形 $\text{[math]}$ 的周长不变

答案解析收藏纠错 + 选题
12. (2023九上·桥西期中) 已知压力F（N）、压强P（Pa）与受力面积S（m²）之间有如下关系式：F＝PS ．当F为定值时，如图中大致表示压强P与受力面积S之间函数关系的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题

13. 小明按照以下步骤画线段AB的三等分点：

画法

图形

1．以A为端点画一条射线；

2．用圆规在射线上依次截取3条等长线段AC、CD、DE ，连接BE；

3．过点C、D分别画BE的平行线，交线段AB于点M、N ， M、N就是线段AB的三等分点．

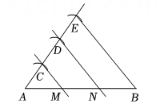这一画图过程体现的数学依据是（）

A . 两直线平行，同位角相等 B . 两条平行线之间的距离处处相等 C . 垂直于同一条直线的两条直线平行 D . 两条直线被一组平行线所截，所得的对应线段成比例

答案解析收藏纠错 + 选题

14. (2023九上·桥西期中) 利用公式解可得一元二次方程式2x²﹣9x+8＝0的两解为a、b ，且a＞b ，则a的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2023九上·桥西期中) 如图1，在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，D是AB上一点，且AD＝2，过点D作DE∥BC交AC于E ，将△ADE绕A点顺时针旋转到图2的位置．则图2中 $\text{[math]}$ 的值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023九上·桥西期中) 抛物线y＝ax²﹣a（a≠0）与直线y＝kx交于A（x₁ ， y₁），B（x₂ ， y₂）两点，若x₁+x₂＜0，则关于直线y＝ax+k；甲答：一定经过一、四象限，乙答：一定经过一、三象限．则正确的是（　　）

A . 甲乙均错 B . 甲乙均对 C . 甲错乙对 D . 甲对乙错

答案解析收藏纠错 + 选题

二、填空题（本大题共3个小题，共10分，17小题2分；18-19小题各4分，每空2分）

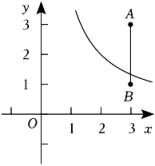
17. 如图，已知点A（3，3），B（3，1），反比例函数 $\text{[math]}$ 图象的一支与线段AB有交点，写出一个符合条件的k的整数值：．

答案解析收藏纠错 + 选题
18. (2023九上·桥西期中) 一个盒子里装有10个红球和若干个白球，这些球除颜色外其余都相同．几名同学轮流从盒子里摸1个球，记录下所摸球的颜色后，再把球放回盒子里搅匀，记录如下：
摸球次数
20
40
60
80
100
120
140
160
180
200
220
240
出现红球的频数
11
23
33
38
49
59
69
81
91
101
109
121
根据以上表格可估计摸到红球的概率为（结果保留小数点后一位），袋中白球约有个．

答案解析收藏纠错 + 选题
19. (2023九上·桥西期中) 如图，折叠矩形ABCD的一边AD ，使D落在BC边上的F处，且 $\text{[math]}$ ．
⑴△AFB与△FEC是否相似？（选填“是”或者“否”）．
⑵若 $\text{[math]}$ 则矩形ABCD的面积为 cm² ．

答案解析收藏纠错 + 选题

三、解答题（本大题共7个小题，共52分，解答应写出文字说明、证明过程或演算步骤）

20. (2023九上·桥西期中) 计算：tan30°﹣2sin60°．

答案解析收藏纠错 + 选题
21. (2023九上·桥西期中) 有三张大小一样而画面不同的画片，先将每一张从中间剪开，分成上下两部分；然后把三张画片的上半部分都放在第一个盒子中，把下半部分都放在第二个盒子中．分别摇匀后，从每个盒子中各随机地摸出一张，求这两张恰好能拼成原来的一幅画的概率．

答案解析收藏纠错 + 选题
22. (2023九上·桥西期中) 教室里的投影仪投影时，可以把投影光线CA ， CB及在黑板上的投影图象高度AB抽象成如图所示的△ABC ， ∠BAC＝90°，黑板上投影图象的高度AB＝120cm ， CB与AB的夹角∠B＝33.7°，求AC的长．（结果精确到1cm ．参考数据：sin33.7°≈0.55，cos33.7°≈0.83，tan33.7°≈0.67）

答案解析收藏纠错 + 选题
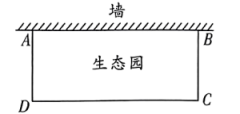
23. (2023九上·广州期中) 为了便于劳动课程的开展，学校打算建一个矩形生态园 $\text{[math]}$ （如图），生态园一面靠墙（墙足够长），另外三面用 $\text{[math]}$ 的篱笆围成．生态园的面积能否为 $\text{[math]}$ ？如果能，请求出 $\text{[math]}$ 的长；如果不能，请说明理由．

答案解析收藏纠错 + 选题
24. (2023九上·桥西期中) 如图，矩形ABCD中，过对角线BD的中点O作BD的垂线EF ，分别交AD ， BC于点E ， F ．判断四边形EBFD的形状，并说明理由．

答案解析收藏纠错 + 选题
25. (2023九上·桥西期中) 在平面直角坐标系xOy中，抛物线y＝ax²﹣4a（a≠0）与x轴的交点为A、B ，（点A在点B的左侧），顶点为C ．
1. （1）求AB的长；
2. （2）若以A、B、C为顶点的三角形为直角三角形，求a的值；
3. （3）横、纵坐标都是整数的点叫做整点，若抛物线在点A ， B之间的部分与线段AB所围成的区域内（不包括边界）恰有1个整点，结合函数的图象，直接写出a的取值范围．
答案解析收藏纠错 + 选题
26. (2023九上·桥西期中) 如图1，在三角形ABC中，角ACB＝90度，AC＝6cm ， BC＝8cm ，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒，连接PQ ．
1. （1）若三角形BPQ与三角形ABC相似，求t的值；
2. （2）直接写出三角形BPQ是等腰三角形时t的值；
3. （3）如图2，连接AQ、CP ，若AQ垂直CP ，求t的值．
答案解析收藏纠错 + 选题