四川省内江市资中县2023-2024学年九年级上学期数学期中...

更新时间：2024-03-15 浏览次数：45 类型：期中考试

一、选择题（本大题共12小题，每小题3分，共36分．每小题只有一个选项符合题意．）

1. (2023九上·资中期中) 下列根式是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·资中期中) 把一元二次方程 $\text{[math]}$ 化为一般形式，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·邯郸月考) 下列各组中的四条线段成比例的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·十堰月考) 关于x的方程 $\text{[math]}$ 实数根的情况，下列判断正确的是（）

A . 有两个相等实数根 B . 有两个不相等实数根 C . 没有实数根 D . 有一个实数根

答案解析收藏纠错 + 选题
5. (2024八上·顺义期中) 若 $\text{[math]}$ ，则（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . x为一切实数

答案解析收藏纠错 + 选题
6. (2023九上·资中期中) 如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在横线上 $\text{[math]}$ 若线段 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·资中期中) 有一个数值转换器，原理如下图所示：当输入的数是324时，输出的结果等于（）

A . 3 B . 18 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·费县模拟) 已知有等腰三角形两边长为一元二次方程x²-3x+2=0的两根，则等腰三角形周长是（）

A . 4 B . 5 C . 4或5 D . 不能确定

答案解析收藏纠错 + 选题
9. (2023九上·资中期中) 手工兴趣小组的同学们将自己制作的书签向本组的其他成员各赠送1个，全组共互赠了30个，如果全组有x名同学，则根据题意列出的方程是（　　）

A . x（x+1）＝30 B . 2x（x+1）＝30 C . x（x-1）＝30 D . x（x-1）＝30×2

答案解析收藏纠错 + 选题
10. (2024九下·浙江模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 用 $\text{[math]}$ 表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023九上·资中期中) 如图是一个按某种规律排列的数阵：根据数阵排列的规律，第6行从左向右数第3个数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023九上·资中期中) 设 $\text{[math]}$ 的两实根为 $\text{[math]}$ ， $\text{[math]}$ ，而以 $\text{[math]}$ ， $\text{[math]}$ 为根的一元二次方程仍是 $\text{[math]}$ ，则数对 $\text{[math]}$ 的个数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，每小题5分，共20分．请将最后答案直接写在答题卷的相应题中的横线上．）

13. (2023九上·资中期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值等于．

答案解析收藏纠错 + 选题
14. (2023九上·固原期末) 已知 $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程，则 $\text{[math]}$ 等于．

答案解析收藏纠错 + 选题
15. (2023九上·资中期中) 如图，从一个大正方形中裁去面积为27和48的两个小正方形，则剩下阴影部分的面积是．

答案解析收藏纠错 + 选题
16. (2023九上·资中期中) 下面这首诗生动的刻画出了周瑜的一生：
大江东去浪淘尽，千古风流数人物；
而立之年督东吴，早逝英年两位数；
十位恰小个位三，个位平方与寿符．(注：而立之年表示人到了30岁)
聪明的同学，你一定能算得出周瑜去世时的年龄是岁．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，共44分）

17. (2023九上·资中期中)
1. （1）计算： $\text{[math]}$ ．
2. （2）解方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023九上·资中期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
19. (2023九上·资中期中) 如图，直线 $\text{[math]}$ 分别交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2023九上·资中期中) 随着粤港澳大湾区建设的加速推进，广东省正加速布局以 $\text{[math]}$ 等为代表的战略性新兴产业，计划到2020年底，全省 $\text{[math]}$ 基站数量将达到6万座，到2022年底，全省 $\text{[math]}$ 基站数量将达到17.34万座
1. （1）按照计划，求2020年底到2022年底，全省 $\text{[math]}$ 基站数量的年平均增长率；
2. （2）若2023年保持前两年 $\text{[math]}$ 基站数量的年平均增长率不变，到2023年底，全省5G基站数量能否超过25万座？
答案解析收藏纠错 + 选题
21. (2023九上·资中期中) 换元法是数学中的一种解题方法．若我们把其中某些部分看成一个整体，用一个新字母代替（即换元），则能使复杂的问题简单化．如：解二元一次方程组 $\text{[math]}$ ，按常规思路解方程组计算量较大．可设 $\text{[math]}$ ， $\text{[math]}$ ，那么方程组可化为 $\text{[math]}$ ，从而将方程组简单化，解出 $\text{[math]}$ 和 $\text{[math]}$ 的值后，再利用 $\text{[math]}$ ， $\text{[math]}$ 解出 $\text{[math]}$ 和 $\text{[math]}$ 的值即可．用上面的思想方法解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题

四、填空题（本大题共4小题，每小题6分，共24分．请将最后答案直接写在答题卷的相应题中的横线上．）

22. (2024八下·凉州月考) 已知，x、y是有理数，且y＝ $\text{[math]}$ + $\text{[math]}$ ﹣4，则2x+3y的立方根为．

答案解析收藏纠错 + 选题
23. (2024七下·泸州期中) 对于实数 $\text{[math]}$ 、 $\text{[math]}$ ，且 $\text{[math]}$ ，我们用符号 $\text{[math]}$ 表示 $\text{[math]}$ 、 $\text{[math]}$ 两数中较小的数，如 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
24. (2023九上·资中期中) 已知 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则代数式 $\text{[math]}$ 的值是

答案解析收藏纠错 + 选题
25. (2023九上·资中期中) 如图是一张矩形纸片 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 中点，点 $\text{[math]}$ 在 $\text{[math]}$ 上，把该纸片沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 的对应点分别为 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 的延长线过点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

五、解答题（本大题共3小题，每小题12分，共36分．解答时必须写出必要的文字说明、证明过程或推演步骤）

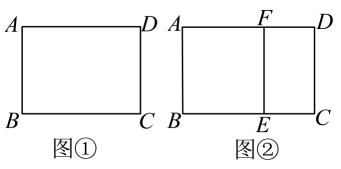
26. (2023九上·资中期中) 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平，它的平面图可看作宽与长的比是 $\text{[math]}$ 的矩形，我们将这种宽与长的比是 $\text{[math]}$ 的矩形叫黄金矩形．如图①，已知黄金矩形 $\text{[math]}$ 的宽 $\text{[math]}$ ．
1. （1）黄金矩形 $\text{[math]}$ 的长 $\text{[math]}$ ；
2. （2）如图②，将图①中的黄金矩形裁剪掉一个以 $\text{[math]}$ 为边的正方形 $\text{[math]}$ ，得到新的矩形 $\text{[math]}$ ，猜想矩形 $\text{[math]}$ 是否为黄金矩形，并证明你的结论；
3. （3）在图②中，连接 $\text{[math]}$ ，求点 $\text{[math]}$ 到线段 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
27. (2023九上·资中期中) 已知 $\text{[math]}$ 、 $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个不相等的实数根．
1. （1）求出 $\text{[math]}$ 的取值范围；
2. （2）若满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
28. (2023九上·资中期中) 阅读与计算，请阅读以下材料，完成相应的任务．
材料：三角形的内角平分线定理：
如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ ．
下面是这个定理的部分证明过程．
证明：如图2，过 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）【思路说明】请按照上面的证明思路，写出该证明的剩余部分；
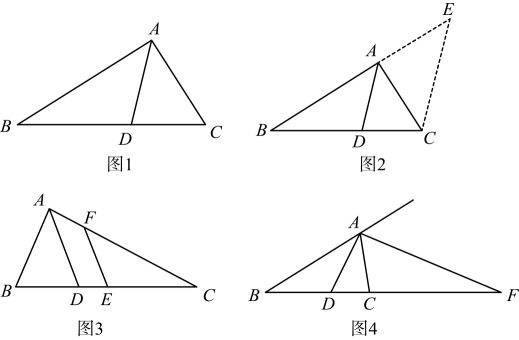
2. （2）【直接应用】如图3， $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 中点， $\text{[math]}$ 是 $\text{[math]}$ 的平分线， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；
3. （3）【拓展延伸】如图4， $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 外角角平分线 $\text{[math]}$ 于点 $\text{[math]}$ ．
  ①找出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 这四条线段的比例关系，并证明；
  ②若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题