云南省曲靖市麒麟区第六中学2022-2023学年九年级下学期...

更新时间：2024-03-12 浏览次数：23 类型：月考试卷

一、选择题 (本大题共 12 个小题，每小题只有一个正确选项，每小题3 分，共 36 分)

1. (2022九下·麒麟月考) 某种药品的说明书上标明保存温度是(20 $\text{[math]}$ 2) ℃，则该药品在哪个范围内保存才合适?（）

A . 18℃~20℃ B . 20℃~22℃ C . 18℃~21℃ D . 18℃~22℃

答案解析收藏纠错 + 选题
2. (2022九下·麒麟月考) 若一个数的倒数是 $\text{[math]}$ ，则这个数的相反数是（）

A . $\text{[math]}$ B . - $\text{[math]}$ C . $\text{[math]}$ D . - $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022九下·麒麟月考) 下列是四届冬奥会微的部分图案，其中既是铀对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九下·麒麟月考) 2022年3月，在第十三届全国人民代表大会第五次会议上，国务院总理李克强在政府工作报告中指出：2021年，我国经济保持恢复发展，国内生产总值达到1140000亿元，增长8.1%.将1140000用科学记数法表示应为（）

A . 0.114x107 B . 1. 14x107 C . 1. 14x106 D . 11. 4x105

答案解析收藏纠错 + 选题
5. (2022九下·麒麟月考) 下列运算中，正确的是（）

A . a⁴.a⁴=a¹⁶ B . a+2a²=3a³ C . a³÷(-a)=-a² D . (-a³)²=a⁵

答案解析收藏纠错 + 选题
6. (2022九下·麒麟月考) 已知ab<0，一次函数y=ax-b与反比例函数y= $\text{[math]}$ 在同一直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022九下·麒麟月考) 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（）

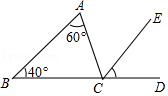
A . 40° B . 45° C . 50° D . 55°

答案解析收藏纠错 + 选题
8. (2022九下·麒麟月考) 如图，在△ABC 中，分别以点 A 和点 C 为圆心，以大于 $\text{[math]}$ AC 的长为半径作弧，两弧相交于 M、N两点；作直线 MN 分别交 BC、AC 于点 D、E若AE=6cm，△ABD 的周长为 26cm，则△ABC 的周长为（）

A . 32cm B . 38cm C . 44cm D . 50cm

答案解析收藏纠错 + 选题
9. (2022九下·麒麟月考) 若方程x²-2x+m=0没有实数根，则m的值可以是（）

A . -1 B . 0 C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九下·麒麟月考) 世界文化遗产“三孔”景区已经完成5G基站布设，“孔夫子家”自此有了 5G网络.5G网络峰值速率为4C网络峰值速率的10倍，在峰值速率下传输500兆数据，5G 网络比4G网络快45秒，求这两种网络的峰值速率.设4C网络的峰值速率为每秒传输x兆数据，依题意，可列方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2022九下·麒麟月考) 按一定规律排列的单项式： x，-3x² ， 9x³ ， -27x⁴ ， 81x⁵.....第n个单项式是（）

A . (-3)^n-1xⁿ B . (-3) ⁿxⁿ⁺¹ C . -3^n-1xⁿ D . (-3)ⁿxⁿ

答案解析收藏纠错 + 选题
12. (2022九下·麒麟月考) 如图所示，在OABC中，AB=AC，动点D在折线段BAC上沿B→A→C方向以每秒1个单位的速度运动，过D垂直于BC的直线交BC边于点E.如果AB=5，BC=8，点D运动的时间为0秒，△BDE 的面积为S，则s关于t的函数图象的大致形状是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题(本大题共4个小题,每小题2分,共8分)

13. (2022九下·麒麟月考) 分解因式：ax²－a=.

答案解析收藏纠错 + 选题
14. (2022九下·麒麟月考) 代数式 $\text{[math]}$ 有意义时， x应满足的条件是.

答案解析收藏纠错 + 选题
15. (2024九下·鼓楼月考) 将一个半径为3的圆形纸片，沿着两条半径剪开形成两个扇形，若其中的一个扇形的面积是6π，则另一个扇形的圆心角的度数是.

答案解析收藏纠错 + 选题
16. (2022九下·麒麟月考) 如图，在边长为6 $\text{[math]}$ 的正六边形ABCDEF中，连接BE， CF，其中点M， N分别为BE和CF上的动点若以M， N， D为顶点的三角形是等边三角形，且边长为整数，则该等边三角形的边长为.

答案解析收藏纠错 + 选题

三、解答题(本大题共8个小题，共56分)

17. (2022九下·麒麟月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022九下·麒麟月考) 已知，如图5， AB=AE，AB//DE， ∠ECB=70°， ∠D=110°，
求证：△ABC≌△EAD.

答案解析收藏纠错 + 选题
19. (2022九下·麒麟月考) 为加强未成年人思想道德建设，某校在学生中开展了“日行一孝”活动，活动设置了四个爱心项目：A项——我为父母过生日，B项——我为父母洗洗脚，C项——我当一天小管家，D项——我与父母谈谈心，要求每个学生必须且只能选择一项参加．为了解全校参加各项目的学生人数，随机抽取了部分学生进行调查，根据调查结果，绘制成如下两幅不完整的统计图，请根据所给信息，解答下列问题：
1. （1）这次抽样调查的样本容量是 ▲ ，补全图①中的条形统计图；
2. （2）在图②的扇形统计图中，B项所占的百分比为m%，则m的值为，C项所在扇形的圆心角α的度数为度；
3. （3）该校参加活动的学生共1200人，请估计该校参加D项的学生有多少人．
答案解析收藏纠错 + 选题
20. (2022九下·麒麟月考) 只有1和它本身两个因数且大于1的正整数叫做素数．我国数学家陈景润从哥德巴赫猜想的研究中取得了世界领先的成果，哥德巴赫猜想是：“每个大于2的偶数都可以表示为两个素数的和”．如20=3+17．
1. （1）若从7、11、19、23这4个素数中随机抽取一个，则抽到的数是7的概率是；
2. （2）从7、11、19、23这4个素数中随机抽取1个数，再从余下的3个数中随机抽取1个数，再用画树状图或列表的方法，求抽到的两个素数之和等于30的概率．
答案解析收藏纠错 + 选题
21. 我市某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励.现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元.
1. （1）求甲、乙两种奖品的单价；
2. （2）根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品的数量不少于乙种奖品数量的 $\text{[math]}$ ，应如何购买才能使总费用最少？并求出最少费用。
答案解析收藏纠错 + 选题
22. (2022九下·麒麟月考) 已知二次函数y=x²-2mx+m²+3(m是常数).
1. （1）求证：不论m为何值，该函数的图象与x轴没有公共点；
2. （2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点?
答案解析收藏纠错 + 选题
23. (2022九下·麒麟月考) 如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
1. （1）判断直线CD和⊙O的位置关系，并说明理由．
2. （2）过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求∠BEC的正切值．
答案解析收藏纠错 + 选题
24. (2022九下·麒麟月考) 如图①，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为对角线 $\text{[math]}$ 上任意一点（不与 $\text{[math]}$ 重合），连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）如图②，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题