四川省绵阳市江油市2023-2024学年八年级上学期期中数学...

更新时间：2024-01-30 浏览次数：23 类型：期中考试

一、选择题：（每小题3分，共36分，每小题给出四个答案中，只有一个符合题目要求，请把你认为正确的题号填入题后面的括号内）

1. (2023八上·江油期中) 下列运算结果正确的是（　　）

A . a²•a⁵＝a¹⁰ B . （﹣2a²）³＝﹣8a⁶ C . 24a³b²÷3ab²＝8a²b D . a²+a³＝a⁵

答案解析收藏纠错 + 选题
2. (2023八上·江油期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ 是（）

A . 锐角三角形 B . 钝角三角形 C . 直角三角形 D . 不能确定

答案解析收藏纠错 + 选题
3. (2023八上·江油期中) 如图，要使一个六边形木架在同一平面内不变形，至少还要钉上木条（）

A . 1根 B . 2根 C . 4根 D . 3根

答案解析收藏纠错 + 选题
4. (2023八上·江油期中) 八角帽又称“红军帽”，是红军的象征，也是中国工农红军军服佩饰最显眼的部分之一，其帽顶近似正八边形．正八边形的一个内角的大小为（　　）

A . 150° B . 140° C . 135° D . 120°

答案解析收藏纠错 + 选题
5. (2023八上·江油期中) 如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的值为（）

A . 3 B . 4 C . 8 D . 2

答案解析收藏纠错 + 选题
6. (2023八上·江油期中) 如图，在△CEF中，∠E＝78°，∠F＝47°，AB∥CF ， AD∥CE ，连接BC ， CD ，则∠A的度数是（　　）

A . 45° B . 47° C . 55° D . 78°

答案解析收藏纠错 + 选题
7. (2023八上·江油期中) 若一个多边形截去一个角后，形成的新多边形的内角和是 $\text{[math]}$ ．则原来多边形的边数可能是（）

A . 10或11 B . 11 C . 11或12 D . 10或11或12

答案解析收藏纠错 + 选题
8. (2023八上·江油期中) 如图，BP是△ABC中∠ABC的平分线，CP是∠ACM的平分线，若∠ABP＝20°，∠ACP＝60°，则∠A﹣∠P＝（　　）

A . 70° B . 60° C . 50° D . 40°

答案解析收藏纠错 + 选题
9. (2023八上·江油期中) 如图，将一个含45°角的直角三角板放在直角坐标系中，三角板两锐角顶点分别落在x轴，y轴上的点A ， B处，直角顶点落在点C（3，3）处，则OA+OB的值为（　　）

A . 4 B . 4.5 C . 6 D . 8

答案解析收藏纠错 + 选题
10. (2023八上·江油期中) 若计算（3x²+2ax+1）•（﹣3x）﹣4x²的结果中不含有x²项，则a的值为（　　）

A . 2 B . 0 C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
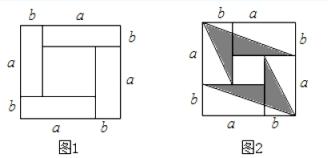
11. (2023八上·江油期中) 小方将4张长为a、宽为b（a＞b）的长方形纸片先按图1所示方式拼成一个边长为（a+b）的正方形，然后按图2所示连接了四条线段，并画出部分阴影图形，若大正方形的面积是图中阴影部分图形面积的3倍，则a、b满足（　　）

A . a＝3b B . 2a＝5b C . a＝2b D . 2a＝3b

答案解析收藏纠错 + 选题
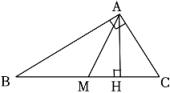
12. (2023八上·江油期中) 如图，在Rt△ABC中，∠BAC＝90°，AH是高，AM是中线，那么在结论①∠B＝∠BAM ， ②∠B＝∠MAH ， ③∠B＝∠CAH ， ④ $\text{[math]}$ ， ⑤S_△_ACH＝S_△_ABM中错误的个数（　　）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题：（本大题共6个小题，每小题3分，共18分.将答案直接填写在题中横线上）.

13. (2023八上·江油期中) 大桥钢架、索道支架、人字梁等为了坚固，都采用三角形结构，这是根据．

答案解析收藏纠错 + 选题
14. (2023八上·江油期中) 如图，直线l₁∥l₂ ，将三角板按如图方式放置，直角顶点在l₂上，若∠1＝36°，则∠2＝．

答案解析收藏纠错 + 选题
15. (2023八上·江油期中) 如图中， $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023八上·江油期中) 已知x+y＝2，xy＝3，则x²y+xy²的值是．

答案解析收藏纠错 + 选题
17. (2023八上·江油期中) 如图，在△ABC内有一点O到△ABC三个顶点的距离相等，连接OA、OB、OC ．若∠BAO＝25°，∠ACO＝55°，则∠BOC的度数为．

答案解析收藏纠错 + 选题
18. (2023八上·江油期中) 已知实数a、b满足a﹣b²＝4，则代数式a²﹣3b²+a﹣14的最小值是．

答案解析收藏纠错 + 选题

三、解答题：（本大题共6个小题，共46分.解答应写出文字说明、证明过程或推理步骤.）

19. (2023八上·江油期中) 计算：
1. （1）计算：28x⁴y²÷7x³y；
2. （2）先化简：再求值，（2x+3y）²﹣（2x+y）（2x﹣y），其中x＝ $\text{[math]}$ ， y＝ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023八上·江油期中) 已知△ABC中，∠B＝∠C ， D为边BC上一点（不与B ， C重合），点E为边AC上一点，∠ADE＝∠AED ， ∠BAC＝44°．
1. （1）求∠C的度数；
2. （2）若∠ADE＝75°，求∠CDE的度数．
答案解析收藏纠错 + 选题
21. (2023八上·江油期中) 化简： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
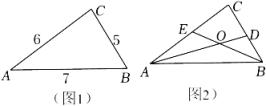
22. (2023八上·江油期中) 我国南宋时期数学家秦九韶（约1202﹣约1261）曾提出利用三角形的三边求面积的秦九韶公式：如果一个三角形的三边长分别为a ， b ， c ，记p＝ $\text{[math]}$ ，那么三角形的面积S＝ $\text{[math]}$ ．在△ABC中，已知BC＝5，AC＝6，AB＝7．
1. （1）如图1，利用秦九韶公式求△ABC的面积；
2. （2）如图2，△ABC的两条角平分线AD ， BE交于点O ，求点O到边AB的距离．
答案解析收藏纠错 + 选题
23. (2023八上·江油期中) 如图，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ，垂足分别是D ， E ． AD＝2.5cm ， DE＝1.7cm ，求BE的长．

答案解析收藏纠错 + 选题
24. (2023八上·江油期中) 如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB ， BE＝BD ，连接AE ， CD ， AE与CD交于点M ， AE与BC交于点N ．
1. （1）求证：AE＝CD；
2. （2）求证：AE⊥CD；
3. （3）连接BM ，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD ，其中正确的一个是　 ▲ 　（请写序号），并给出证明过程．
答案解析收藏纠错 + 选题