一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.
-
A . 3
B . a
C . 
D . 
-
A . 系数是
， 次数是3
B . 系数是- ， 次数是5
C . 系数是- ， 次数是3
D . 系数是5，次数是-
-
A . 1
B . 0
C . -
D . -2
-
4.
(2023七上·南明期中)
在记录某水库的水位时，将80 m作为标准水位，水位为85.3 m记为+5.3 m，则水位为 76.8 m 应记为（ ）
A . +76.8 m
B . -76.8 m
C . +3.2 m
D . -3.2 m
-
A . 4x+6=-8移项，得4x=-8+6
B . 
x-3=
+1去分母，得6x-42=7x+1
C . -
x=6系数化为1，得x=12
D . 9-5(2-3x)=0去括号，得9-10+15x=0
-
6.
(2023七上·南明期中)
如图所示，在一个三阶幻方中，填写了一些数、式子和汉字(其中每个式子或汉字都表示一个数)，若处于每一横行、每一竖列，以及两条斜对角线上的3个数之和都相等，则这个幻方中m的值为（ ）
A . 3
B . 1
C . -8
D . -10
-
A . 1，-1
B . 1，2
C . 1，-2
D . 1，1
-
A . -1
B . 1
C . 2
D . -2
-
9.
(2023七上·南明期中)
小南在解关于x的一元一次方程
-m=
时，由于粗心大意在去分母时出现漏乘错误，把原方程化为4x-m=3，并解得x=1，请根据以上已知条件求出原方程正确的解为（ ）
A . x=
B . x=1
C . x=
D . x=-
-
A . 1
B . -1
C . 2
D . -2
-
11.
(2024七上·三台期末)
我国古代数学著作《孙子算经》中有这样一道题，原文如下：今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽，问：城中家几何？大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完，问：城中有多少户人家？在这个问题中，城中人家的户数为（ ）
A . 25
B . 75
C . 81
D . 90
-
12.
(2023七上·南明期中)
在长方形ABCD中，放入5个形状大小相同的小长方形(空白部分)，其中AB=7 cm，BC=11 cm，则阴影部分图形的总面积为（ ）
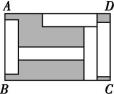
A . 18 cm2
B . 21 cm2
C . 24 cm2
D . 27 cm2
二、填空题:本大题4小题,每小题4分,共16分.
-
-
-
15.
(2023七上·南明期中)
扬州雕版印刷技艺历史悠久，元代数学家朱世杰的《算学启蒙》一书曾刻于扬州，该书是中国较早的数学著作之一，书中记载一道问题：“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天追上慢马？答：快马
天追上慢马.
-
16.
(2023七上·南明期中)
已知代数式mx+2m，当x取某些值时，代数式mx+2m对应的值如表所示.
x | -1 | -0.5 | 0 | 0.5 | 1 |
mx+2m | 1 | 1.5 | 2 | 2.5 | 3 |
则关于x的方程2mx+4m-3=0的解为x=.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
-
-
（2）
=
-3.
-
-
19.
(2023七上·南明期中)
已知方程①：2-3(x+1)=0，方程②：
-3k-2=2x.若方程①与方程②的解互为倒数，求k的值.
-
20.
(2023七上·南明期中)
一张学生课桌由一个桌面和四条桌腿组成，若1 m
3木料可制作桌面50个或桌腿300条，现有15 m
3木料，请你设计一下用多少木料做桌面，用多少木料做桌腿，恰好配套.
-
21.
(2023七上·南明期中)
我们规定：若关于x的一元一次方程a+x=b(a≠0)的解为x=
， 则称该方程为“商解方程”.例如：2+x=4的解为x=2且x=
， 则方程2+x=4是“商解方程”.请回答下列问题：
-
（1）
判断4+x=
是不是“商解方程”，并说明理由；
-
（2）
若关于x的一元一次方程6+x=m+3是“商解方程”，求m的值.
-
-
（1）
该校八年级每一个班要赛场；若有n个班比赛，则每一个班要赛场.
-
（2）
规则为每班胜一场得3分，平一场得1分，负一场得0分.若八年级(1)班球队已经踢完所有比赛，其中平的场数是负的场数的2倍，共得17分，该球队胜了几场球?
-
23.
(2023七上·南明期中)
为了增强市民的节约用水意识，自来水公司实行阶梯收费，具体情况如表：
每月用水量 | 收费 |
不超过10吨的部分 | 水费1.5元/吨 |
10吨以上至20吨的部分 | 水费2元/吨 |
20吨以上的部分 | 水费2.4元/吨 |
-
（1）
若小刚家6月份用水8吨，则小刚家6月份应缴水费元(直接写出结果).
-
（2）
若小刚家7月份的水费为21元，则小刚家7月份的用水量为多
少吨?
-
（3）
若小刚家8月、9月共用水20吨，9月底共缴两个月水费合计
32元.已知8月份用水不超过10吨，求小刚家8、9月各用多少吨水?
-
24.
(2023七上·南明期中)
某厂接到一所中学的冬季校服制作任务，计划用A，B两台大型设备进行加工.如果单独用A型设备需要90天做完；如果单独用B型设备需要60天做完.为了同学们能及时领到冬季校服，工厂决定由两台设备同时赶制.
-
-
（2）
若两台设备同时加工30天后，B型设备出了故障，暂时不能工作，此时离发冬季校服时间还有13天.如果由A型设备单独完成剩下的任务，会不会影响学校发校服的时间?请通过计算说明理由.
-
25.
(2024七上·上城期末)
第24届冬奥会于2022年2月4日在北京举行，某经销商在冬奥会前预测带有“冰墩墩”吉祥物标志的甲、乙两种纪念品可能会畅销，于是，该经销商用6 200元一次性购进了甲、乙两种纪念品共100件.已知甲、乙两种纪念品的进价和售价如表：
种类 | 进价(元/件) | 售价(元/件) |
甲 | 50 | 100 |
乙 | 70 | 90 |
-
（1）
该经销商一次性购进甲、乙两种纪念品各多少件?
-
（2）
如果在北京冬奥会开幕式当天销售完全部纪念品，则可获得利润为多少元?
-
（3）
根据预测的销售情况，该经销商会再次以相同的进价购进甲、乙两种纪念品，已知甲种纪念品的数量是第一次购进甲种纪念品数量的2倍，乙种纪念品的数量与第一次所购乙种纪念品数量相同.如果甲种纪念品打折销售，乙种纪念品按原价销售，全部销售完后所获的利润正好比第一次获得的利润多1 200元，则甲种纪念品应按原价打几折销售?
