
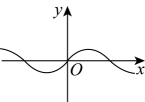
 B .
B . 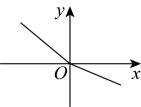 C .
C . 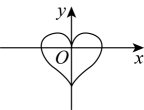 D .
D . 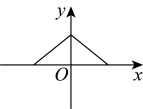
 B .
B .  C .
C .  D .
D . 
x | … | 0 | 1 | 2 | … | |||
y | … | 9 | 5 | 1 | … |
| 山西省居民电价表 | |||
用户分类 | 分档 | 电量(度) | 电价(元/度) | 执行周期 |
一户一表 居民用户 | 第一档 |
| 0.477 | 居民阶梯电价以“双月”为周期执行 |
第二档 |
| 0.527 | ||
第三档 | 521及以上 (双月电量521度及以上) | 0.777 | ||



| 宸宸 | 琮琮 | 莲莲 |
进价(元/个) | 60 | 65 | 70 |
售价(元/个) | 90 | 90 | 90 |
如图 ,
,
, 过点
作
于点
, 过点
作
于点
. 则
. 我们把这个数学模型称为“
字”模型或“一线三等角”模型.
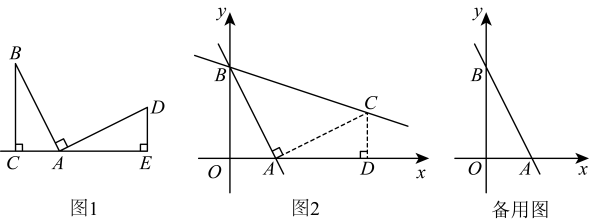
【模型应用】
在平面直角坐标系中,直线与
轴交于点
, 与
轴交于点
.
小明想利用“一线三等角”模型解决这个问题.如图,过点作
的垂线交
于点
, 再过点
作
轴的垂线,垂足为
, 可求出点
的坐标为,从而求得直线
的表达式为.
小许是个爱动脑筋的学生,她在学习了二元一次方程组后遇到了这样一道题目:如图1,长方形中放置
个形状和大小都相同的小长方形(尺寸如图
),求图中阴影部分的面积.
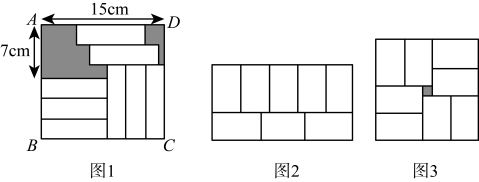
请按照小许的思路完成上述问题:
动手实践:解决完上面的问题后,小许在家里找了张形状大小都相同的卡片,恰好拼成了一个大的长方形如图
所示,打乱后又拼成如图
那样的大正方形,中间还留了一个洞,恰好是边长为
的小正方形,求每个小长方形的面积.请给出解答过程.