四川省成都市龙泉驿区东竞高级中学2023-2024学年高一上...

更新时间：2024-01-29 浏览次数：41 类型：月考试卷

一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的.

1. (2023高一上·龙泉驿月考) 已知集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高一上·龙泉驿月考) “ $\text{[math]}$ ”是“ $\text{[math]}$ ” 的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分又不必要条件

答案解析收藏纠错 + 选题
3. (2023高一上·龙泉驿月考) 设函数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 2 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高一上·龙泉驿月考) 已知扇形的圆心角为 $\text{[math]}$ ，弧长为 $\text{[math]}$ ，则扇形的半径为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 6

答案解析收藏纠错 + 选题
5. (2023高一上·龙泉驿月考) 已知角 $\text{[math]}$ 的终边经过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高一上·龙泉驿月考) 函数 $\text{[math]}$ 的零点所在区间是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高一上·龙泉驿月考) 为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯在公元前二世纪首先提出了星等这个概念.星等的数值越小，星星就越亮；星等的数值越大它的光就越暗.到了 1850 年，由于光度计在天体光度测量的应用，英国天文学家普森又提出了亮度的概念，天体的明暗程度可以用星等或亮度来描述. 两颗星的星等与亮度满足 $\text{[math]}$ ，其中星等为 $\text{[math]}$ 的星的亮度为 $\text{[math]}$ . 已知“心宿二”的星等是 1， “天津四”的星等是 1.25 ，则“心宿二”的亮度大约是“天津四”的（）倍.

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高一上·龙泉驿月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题: 本题共 4 小题, 每小题 5 分, 共 20 分. 在每小题给出的选项中, 有多项符合题目要求. 全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分.

9. (2023高一上·龙泉驿月考) 已知下列各角： (1) $\text{[math]}$ ： (2) $\text{[math]}$ ； (3) $\text{[math]}$ ； (4) $\text{[math]}$ ，其中是第二象限角的是（）

A . (1) B . (2) C . (3) D . (4)

答案解析收藏纠错 + 选题
10. (2023高一上·龙泉驿月考) 下列四个式子中： (1) $\text{[math]}$ ； (2)若 $\text{[math]}$ ，则 $\text{[math]}$ ； (3) $\text{[math]}$ ； (4) $\text{[math]}$ . 其中正确的有（）

A . (1) B . (2) C . (3) D . (4)

答案解析收藏纠错 + 选题
11. (2024高一上·广州期中) 若 $\text{[math]}$ 是定义域为 $\text{[math]}$ 的偶函数，且 $\text{[math]}$ 在 $\text{[math]}$ 上为减函数，则下列选项正确的是（）

A . $\text{[math]}$ 的图象关于 $\text{[math]}$ 轴对称 B . $\text{[math]}$ 在 $\text{[math]}$ 上为减函数 C . 当 $\text{[math]}$ 时， $\text{[math]}$ 取得最大值 D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高一上·龙泉驿月考) 已知函数 $\text{[math]}$ . 则下列说法正确的是（）

A . 函数 $\text{[math]}$ 与函数 $\text{[math]}$ 互为反函数 B . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 内没有零点 C . 若 $\text{[math]}$ 均为正实数，且满足 $\text{[math]}$ ，则 $\text{[math]}$ D . 若函数 $\text{[math]}$ 的图象与函数 $\text{[math]}$ 的图象和函数 $\text{[math]}$ 的图象在第一象限内交点的横坐标分别为 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题: 本题共 4 小题, 每小题 5 分, 共 20 分. 请将答案填写在答题卡相应位置上.

13. (2023高一上·龙泉驿月考) 若 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2023高一上·龙泉驿月考) 化简： $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2023高一上·龙泉驿月考) 已知函数 $\text{[math]}$ ，则 $\text{[math]}$ 的值域为

答案解析收藏纠错 + 选题
16. (2023高一上·龙泉驿月考) 函数 $\text{[math]}$ ，方程 $\text{[math]}$ 有 3 个实数解，则 $\text{[math]}$ 的取值范围为

答案解析收藏纠错 + 选题

四、解答题: 本题共 6 小题, 共 70 分.解答应写出文字说明、证明过程或演算步骤.

17. (2023高一上·龙泉驿月考) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023高一上·龙泉驿月考) 设集合 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
19. (2023高一上·龙泉驿月考)
1. （1）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
20. (2023高一上·龙泉驿月考) 已知指数函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 的解析式并判断 $\text{[math]}$ 的单调性；
2. （2）函数 $\text{[math]}$ ，求函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上的最小值。
答案解析收藏纠错 + 选题
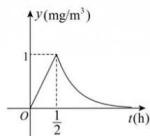
21. (2023高一上·龙泉驿月考) 秋冬季是流感的高发季节，为了预防流感，东竞高中决定对教室采用药熏消毒法进行消毒，药熏开始前要求学生全部离开教室.已知在药熏过程中，教室内每立方米空气中的药物含量 $\text{[math]}$ (毫克) 与药熏时间 $\text{[math]}$ (小时) 成正比：当药熏过程结束，药物即释放完毕，教室内每立方米空气中的药物含量 $\text{[math]}$ (毫克) 达到最大值.此后，教室内每立方米空气中的药物含量 $\text{[math]}$ (毫克) 与时间 $\text{[math]}$ (小时) 的函数关系式为 $\text{[math]}$ ( $\text{[math]}$ 为常数， $\text{[math]}$ ). 已知从药熏开始，教室内每立方米空气中的药物含量 $\text{[math]}$ (毫克) 关于时间 $\text{[math]}$ (小时) 的变化曲线如图所示.
1. （1）从药熏开始，求每立方米空气中的药物含量 $\text{[math]}$ (毫克) 与时间 $\text{[math]}$ (小时) 之间的函数关系式；
2. （2）据测定，当空气中每立方米的药物含量不高于 $\text{[math]}$ 毫克时，学生方可进入教室，那么从药薰开始，至少需要经过多少小时后，学生才能回到教室.
答案解析收藏纠错 + 选题
22. (2023高一上·龙泉驿月考) 已知函数 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，求不等式 $\text{[math]}$ 的解集；
2. （2）已知函数 $\text{[math]}$ ，且方程 $\text{[math]}$ 有唯一实数解，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题