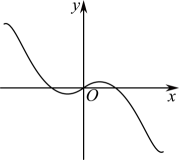
 B .
B . 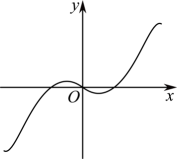 C .
C . 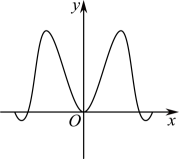 D .
D . 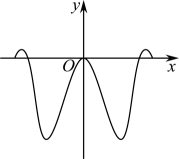
0 | 1 | 0.5 | 0.75 | 0.625 | 0.5625 | 0.6875 | 0.65625 | 0.671875 | |
-1 | 1 | -0.375 | 0.1718 | -0.1308 | -0.2595 | 0.01245 | -0.06113 | -0.02483 |
要使零点的近似值精确到0.1,则对区间
的最少等分次数和近似解分别为( )

1 | 2 | 3 | 4 | 5 | 6 | … | |
| … | 6 | … | 36 | … | 216 | … |
若奥密克戎变异株的感染人数y与经过个单位时间T的关系有两个函数模型
与
可供选择.
(参考数据: ,
,
,
)