一、选择题(本大题共14个小题,共38分,1~10小题每小题3分,11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A . 9
B . -3
C . 3
D . -9
-
-
-
-
-
A . 6个a相乘
B . a的6倍
C . 6个a相加
D . 6的a倍
-
-
8.
(2023七上·信都月考)
如图,用剪刀沿直线将一片平整的树叶剪掉一部分,则剩下的树叶周长小于原树叶的周长,能解释这一现象的数学道理是( )

A . 一条线段只有一个中点
B . 两点之间,线段最短
C . 经过已知两点有且只有一条直线
D . 经过一点有无数条直线
-
-
-
A . 它的值比 小
B . 它的值比3小
C . 它的值比3大
D . 它的值随着
小
B . 它的值比3小
C . 它的值比3大
D . 它的值随着 的增大而增大
的增大而增大
-
A . 在线段MP上
B . 在线段PN上
C . 在点M的左侧
D . 在点N的右侧
-
13.
(2023七上·信都月考)
如图,如果将地球分为水半球和陆半球,已知水半球
海洋面积占

, 陆半球
陆地面积占

, 若设地球总面积为
m , 且两半球面积相等,则地球
陆地总面积可表示为( )

-
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
-
-
16.
(2023七上·信都月考)
仔细观察下列等式:
第1个: ; 第2个:
; 第2个: ;
;
第3个: ; 第4个:
; 第4个: ;
;
…
这些等式反映出正整数间的某种运算规律,按要求解答下列各题:
⑴ 请你写出第5个等式:.
⑵若 为正整数,则第
为正整数,则第 个等式可表示为.
个等式可表示为.
-
17.
(2023七上·信都月考)
在登山过程中,海拔每升高1千米,气温下降

. 已知某登山大本营所在的位置的气温是

, 登山队员从大本营出发登山.当海拔升高

千米时,所在位置的气温是

, 那么用

表示

的式子是
;海拔4.5千米的气温是

.
三、解答题(本大题共七个小题满分72分,解答题应写出必要的解题步骤或文字说明)
-
-
-
(1)

的度数;
-
(2)

的度数.
-
-
(1)

;
-
(2)

.
-
21.
(2023七上·信都月考)
为保障校园体育活动安全有序的开展,学校计划利用假期在足球场四周安装安全防护栏,平面示意图如图2所示,假如每张防护栏长2.5米,每两张防护栏中间加装一个立柱进行加固,每根立柱宽为0.2米.

-
(1)
根据上图及图中所含的规律,将表格补充完整.
立柱根数 | 1 | 2 | 3 | 4 | 5 | … |
护栏总长度(米) | 0.2 | 2.9 | | 8.3 | | … |
-
(2)
设立柱根数为

, 请用含

的代数式表示护栏总长度,并求出当把

时,护栏的总长度.
-
-
-
(2)
假设小美给出的三位数的百位数字为a , 个位数字是b , 请解释其中的原因.
-
23.
(2023七上·信都月考)
坤铭家有一块长方形菜地,长48米,宽40米.菜地中间欲铺设横、纵两条道路(图中空白部分),如图1所示,纵向道路的宽是横向道路的宽的2倍,设横向道路的宽是
x米(
x>0).
-
(1)
填空:在图1中,纵向道路的宽是
米;(用含
x的代数式表示)

-
-
(3)
若把横向道路的宽改为原来的2.2倍,纵向道路的宽改为原来的一半,如图2所示,设图1与图2中菜地的面积(阴影部分)分别为

,

, 试比较

与

的大小.
-
-
(1)
若

时
①当 时,求整式
时,求整式 的值;
的值;
②若多项式 的值与
的值与 的取值无关,求
的取值无关,求 的值;
的值;
-
(2)
当

时,多项式

的值为21,求当

时,多项式

的值.
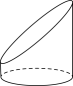 B .
B . 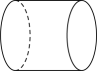 C .
C . 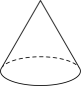 D .
D . 
 B .
B .  C .
C .  D .
D . 

![]()
; 第2个:
;
; 第4个:
;
为正整数,则第
个等式可表示为.



时,求整式
的值;
的值与
的取值无关,求
的值;