山西省阳泉市平定县第二中学校2023-2024学年九年级上学...

更新时间：2024-02-22 浏览次数：21 类型：期中考试

一、选择题（本大题共16个小题，共38分，1～6小题各3分，7-16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2023九上·平定期中) 下列函数不属于二次函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023九上·平定期中) 下列一元二次方程中，没有实数根的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·正定模拟) 一元二次方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . 无实数解

答案解析收藏纠错 + 选题
4. (2023九上·平定期中) 下列配方中，变形正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·平定期中) 顶点坐标为 $\text{[math]}$ ，开口方向和大小与抛物线 $\text{[math]}$ 相同的抛物线为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·平定期中) 等腰三角形的底和腰是方程 $\text{[math]}$ 的两个根，则这个三角形的周长为（）

A . 7 B . 8 C . 7或8 D . 不能确定

答案解析收藏纠错 + 选题
7. (2023九上·平定期中) 已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 和 $\text{[math]}$ 两点，则m的值为（）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·平定期中) 抛物线 $\text{[math]}$ 上有两点 $\text{[math]}$ ， $\text{[math]}$ ．嘉嘉说：“若 $\text{[math]}$ ，则 $\text{[math]}$ ”；琪琪说：“若 $\text{[math]}$ ，则 $\text{[math]}$ ”．对于他们的说法，正确的是（）

A . 嘉嘉正确，琪琪错误 B . 琪琪正确，嘉嘉错误 C . 他们说的都正确 D . 他们说的都不正确

答案解析收藏纠错 + 选题
9. (2023九上·平定期中) 已知关于x的方程 $\text{[math]}$ 的两根分别为 $\text{[math]}$ ， $\text{[math]}$ ，且满足 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·平定期中) 要得到二次函数 $\text{[math]}$ 的图象，需将 $\text{[math]}$ 的图象（）

A . 向左平移1个单位，再向下平移3个单位 B . 向右平移1个单位，再向上平移3个单位 C . 向左平移1个单位，再向上平移2个单位 D . 向右平移1个单位，再向下平移2个单位

答案解析收藏纠错 + 选题
11. (2023九上·平定期中) 一个两位数，它的十位上的数字比个位上的数字小2，个位数字与十位数字的平方和比这个两位数小1，则这个两位数是（）

A . 24 B . 13 C . 46 D . 35

答案解析收藏纠错 + 选题
12. (2023九上·平定期中) 如图，抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ ，下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 当 $\text{[math]}$ 时，y随x的增大而增大 D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2023九上·平定期中) 二次函数y＝ax²+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
14. (2023九上·平定期中) 已知二次函数 $\text{[math]}$ ，对于任意的x值， $\text{[math]}$ 恒成立，则a的值可以是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
15. (2023九上·平定期中) 把一个足球垂直于水平地面向上踢，时间为t（秒）时该足球距离地面的高度h（米）适用公式 $\text{[math]}$ ．若存在两个不同的t的值，使足球离地面的高度均为a米，则a的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023九上·平定期中) 如图，A ， B ， C ， D为矩形的四个顶点， $\text{[math]}$ ， $\text{[math]}$ ，动点P ， Q分别从点A ， C同时出发，点P以 $\text{[math]}$ 的速度向点B移动，一直到达点B为止，点Q以 $\text{[math]}$ 的速度向点D移动，当点P到达点B时，点Q也随之停止运动，设点P的运动时间为 $\text{[math]}$ ．当 $\text{[math]}$ 时，t的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共3个小题，共10分，17小题2分，18～19小题各4分，每空2分，把答案写在题中横线上）

17. (2023九上·平定期中) 已知抛物线 $\text{[math]}$ 的对称轴是 $\text{[math]}$ ，若关于x的方程 $\text{[math]}$ 的一个根是3，那么该方程的另一个根是．

答案解析收藏纠错 + 选题
18. (2023九上·平定期中) 已知关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则m的取值范围为，若方程两根a ， b满足 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2023九上·平定期中) 如图，已知抛物线 $\text{[math]}$ ．

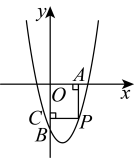
⑴抛物线与y轴的交点B的坐标为；
⑵P是抛物线 $\text{[math]}$ 在第四象限上的一点，过点P分别向x轴和y轴作垂线，垂足分别为点A、C ，则四边形 $\text{[math]}$ 周长的最大值为．

答案解析收藏纠错 + 选题

三、解答题（本大题共7个小题，共72分，解答应写出文字说明、证明过程或演算步骤）

20. (2023九上·平定期中) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2023九上·平定期中) 已知关于x的一元二次方程 $\text{[math]}$ ．
1. （1）求证：不论m为何值，方程总有两个不相等的实数根；
2. （2）设 $\text{[math]}$ ， $\text{[math]}$ 是方程的两个根，且 $\text{[math]}$ ，求m的值．
答案解析收藏纠错 + 选题
22. (2023九上·平定期中) 如图，在平面直角坐标系中，二次函数 $\text{[math]}$ （b ， c是常数）的图象与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求这个二次函数的表达式及其顶点坐标；
2. （2）当 $\text{[math]}$ 时，求y的取值范围．
答案解析收藏纠错 + 选题
23. (2023九上·平定期中) 如图，一位篮球运动员跳起投篮，篮球的运动路线是抛物线 $\text{[math]}$ 的一部分，若这次投篮正好命中篮筐中心，已知篮筐的中心离地面的距离为 $\text{[math]}$ ．
1. （1）他的脚底与篮筐中心正下方的距离l是多少 $\text{[math]}$ ？
2. （2）若对方一名球员想对此球进行成功盖帽，已知该球员的弹跳高度可达 $\text{[math]}$ ，那么他应该在离投篮运动员多远的地方起跳？
答案解析收藏纠错 + 选题
24. (2023九上·平定期中) 某农场要建一个饲养场（矩形 $\text{[math]}$ ），两面靠墙（ $\text{[math]}$ 位置的墙最大可用长度为25m， $\text{[math]}$ 位置的墙最大可用长度为21m），另外两边用木栏围成，中间用木栏隔成两个小矩形并在如图所示的两处各留1m宽的门（不用木栏），建成后木栏总长50m．
1. （1）若饲养场（矩形 $\text{[math]}$ ）的面积为 $\text{[math]}$ ，求边 $\text{[math]}$ 的长；
2. （2）小芳说：“饲养场的面积最多能达到 $\text{[math]}$ ． ”若能达到，求出边 $\text{[math]}$ 的长；若不能达到，请说明理由．
答案解析收藏纠错 + 选题
25. (2023九上·平定期中) 某水果店购进一批水果，进价为10元/千克，售价不低于16元/千克，且不超过35元/千克，根据销售情况，发现该水果在一天内的销售量y（千克）与该天的售价x（元/千克）之间的关系满足下表所示的一次函数关系．
销售量y（千克）
…
32
30
26
24
…
售价x（元/千克）
…
18
20
24
26
…
1. （1）若某天这种水果售价为28元/千克，求当天该水果的销售量；
2. （2）设某天销售这种水果获利W元，写出W与售价x之间的函数关系式；如果水果店该天获利400元，那么这天水果的售价为多少元？
答案解析收藏纠错 + 选题
26. (2023九上·平定期中) 如图，已知抛物线L： $\text{[math]}$ 与x轴相交于A、B两点，与y轴交于点C ，点 $\text{[math]}$ 是x轴上的动点．
1. （1）小华同学在研究了抛物线L的解析式后，得出下面的结论：因为m是任意实数，所以点C可以在y轴上任意移动，即点C可以在y轴任意位置上，你认为他的结论有道理吗？说说你的想法．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，
  ①求m的值；
  ②若 $\text{[math]}$ ，过点N作x轴的垂线交抛物线于点P ，交直线 $\text{[math]}$ 于点G ，当 $\text{[math]}$ 时，求n的值．
答案解析收藏纠错 + 选题