山东省潍坊市安丘市2023-2024学年高三上学期期末适应性...

更新时间：2024-02-27 浏览次数：21 类型：期末考试

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2024·潍坊期末) 若集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的一个必要不充分条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·潍坊期末) 江南的周庄、同里、甪直、西塘、乌镇、南浔古镇，并称为“江南六大古镇”，是中国江南水乡风貌最具代表的城镇，它们以其深邃的历史文化底蕴、清丽婉约的水乡古镇风貌、古朴的吴侬软语民俗风情，在世界上独树一帜，驰名中外.这六大古镇中，其中在苏州境内的有3处.某家庭计划今年暑假从这6个古镇中挑选2个去旅游，则只选一个苏州古镇的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·潍坊期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若存在非零实数 $\text{[math]}$ 使得 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 8 B . 9 C . 10 D . 12

答案解析收藏纠错 + 选题
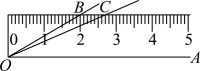
5. (2024·潍坊期末) 如图，将 $\text{[math]}$ 的 $\text{[math]}$ 按下面的方式放置在一把刻度尺上，顶点 $\text{[math]}$ 与尺下沿的端点重合， $\text{[math]}$ 与尺下沿重合， $\text{[math]}$ 与尺上沿的交点 $\text{[math]}$ 在尺上的读数为 $\text{[math]}$ ，若按相同的方式将 $\text{[math]}$ 的 $\text{[math]}$ 放置在该刻度尺上，则 $\text{[math]}$ 与尺上沿的交点 $\text{[math]}$ 在尺上的读数与下列哪项最接近（）（结果精确到 $\text{[math]}$ ，参考数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·潍坊期末) 已知函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的两个零点分别为 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个数适当调整顺序后可为等差数列，也可为等比数列，则不等式 $\text{[math]}$ 的解集为

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·潍坊期末) 已知 $\text{[math]}$ 是双曲线 $\text{[math]}$ 的左焦点， $\text{[math]}$ 为坐标原点，过点 $\text{[math]}$ 且斜率为 $\text{[math]}$ 的直线与 $\text{[math]}$ 的右支交于点 $\text{[math]}$ ，则 $\text{[math]}$ 的离心率为（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. (2024·潍坊期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有错选的得0分．

9. (2024·潍坊期末) 已知复数 $\text{[math]}$ 则（）

A . $\text{[math]}$ B . z₁，z₂，z₃的实部依次成等比数列 C . $\text{[math]}$ D . $\text{[math]}$ 的虚部依次成等差数列

答案解析收藏纠错 + 选题
10. (2024·潍坊期末) 2022年11月，国内猪肉、鸡蛋、鲜果、禽肉、粮食、食用油、鲜菜价格同比（与去年同期相比）的变化情况如图所示，则下列说法不正确的是（）

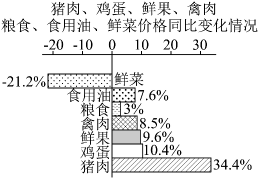
A . 猪肉、鸡蛋、鲜果、禽肉、粮食、食用油这6种食品中，食用油价格同比涨幅最小. B . 这7种食品价格同比涨幅的平均值超过 $\text{[math]}$ C . 去年11月鲜菜价格要比今年11月低 D . 猪肉价格同比涨幅超过禽肉价格同比涨幅的5倍

答案解析收藏纠错 + 选题
11. (2024·潍坊期末) 在正四棱台 $\text{[math]}$ 中， $\text{[math]}$ 则

A . 该正四棱台的体积为 $\text{[math]}$ B . 直线 $\text{[math]}$ 与底面 $\text{[math]}$ 所成的角为60° C . 线段 $\text{[math]}$ 的长为 $\text{[math]}$ D . 以 $\text{[math]}$ 为球心，且表面积为 6π的球与底面 $\text{[math]}$ 相切

答案解析收藏纠错 + 选题
12. (2024·潍坊期末) 已知直线l与抛物线E： $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，其中 $\text{[math]}$ ， $\text{[math]}$ ．分别过A ， B作抛物线准线的垂线，垂足分别C ， D ，线段AB的中点到准线的距离为d ，则下列命题正确的是

A . 若直线l过抛物线的焦点F ，则焦点F在以线段CD为直径的圆外 B . 若直线l过抛物线的焦点F ，则 $\text{[math]}$ 的最小值为 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则△ABF的面积的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分．

13. (2024·潍坊期末) 某校期末统考数学成绩服从正态分布 $\text{[math]}$ ．按 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的比例将考试成绩划为 $\text{[math]}$ 四个等级，其中分数大于或等于83分的为 $\text{[math]}$ 等级，则 $\text{[math]}$ 等级的分数应为．（用区间表示）

答案解析收藏纠错 + 选题
14. (2024·潍坊期末) 已知 $\text{[math]}$ 的二项式系数之和为256，则其展开式中 $\text{[math]}$ 的系数为.

答案解析收藏纠错 + 选题
15. (2024·潍坊期末) 已知圆 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线l与圆O交于P、Q两点，则 $\text{[math]}$ 的最小值等于．

答案解析收藏纠错 + 选题
16. (2024·潍坊期末) 某公园有一个坐落在水平地面上的大型石雕，如图是该石雕的直观图.已知该石雕是正方体截去一个三棱锥后剩余部分， $\text{[math]}$ 是该石雕与地面的接触面，其中 $\text{[math]}$ 是该石雕所在正方体的一个顶点.某兴趣小组通过测量 $\text{[math]}$ 的三边长度，来计算该正方体石雕的相关数据.已知测得 $\text{[math]}$ ，则该石雕最高点 $\text{[math]}$ 到地面的距离为 $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤.

17. (2024·潍坊期末) $\text{[math]}$ 的内角A ， B ， C所对的边分别为a ， b ， c ，且 $\text{[math]}$ .
1. （1）求角 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
18. (2024·潍坊期末) 已知S_n ，为等比数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和， $\text{[math]}$ ，且 $\text{[math]}$
1. （1）若 $\text{[math]}$ 为等差数列，求数列 $\text{[math]}$ 的通项公式；
2. （2）若 $\text{[math]}$ 为等比数列， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2024·潍坊期末) 如图，在三棱锥 P-ABC中，平面 PAB⊥平面ABC，AB=4，BC=2，AC=PA=PB=2 $\text{[math]}$ ， D，E分别为PC，PA的中点.
1. （1）证明：平面 BCE⊥平面 PAB.
2. （2）求平面 PBC与平面BDE 的夹角的余弦值.
答案解析收藏纠错 + 选题
20. (2024·潍坊期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的单调区间；
2. （2）令 $\text{[math]}$ ，若 $\text{[math]}$ ，函数 $\text{[math]}$ 有两个零点，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
21. (2024·潍坊期末) 某中学的风筝兴趣小组决定举行一次盲盒风筝比赛，比赛采取得分制度评选优胜者，可选择的风筝为硬翅风筝､软翅风筝､串式风筝､板式风筝､立体风筝，共有5种风筝，将风筝装入盲盒中摸取风筝，每位参赛选手摸取硬翅风筝或软翅风筝均得1分并放飞风筝，摸取串式风筝､板式风筝､立体风筝均得2分并放飞风筝，每次摸取风筝的结果相互独立，且每次只能摸取1只风筝，每位选手每次摸取硬翅风筝或软翅风筝的概率为 $\text{[math]}$ ，摸取其余3种风筝的概率为 $\text{[math]}$ .
1. （1）若选手甲连续摸了2次盲盒，其总得分为 $\text{[math]}$ 分，求 $\text{[math]}$ 的分布列与期望；
2. （2）假设选手乙可持续摸取盲盒，即摸取盲盒的次数可以为 $\text{[math]}$ 中的任意一个数，记乙累计得 $\text{[math]}$ 分的概率为 $\text{[math]}$ ，当 $\text{[math]}$ 时，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
22. (2024·潍坊期末) 已知圆 $\text{[math]}$ ，点 $\text{[math]}$ ， P是圆M上的动点，线段PN的中垂线与直线PM交于点Q ，点Q的轨迹为曲线C ．
1. （1）求曲线C的方程；
2. （2） $\text{[math]}$ ，点E、F（不在曲线C上）是直线 $\text{[math]}$ 上关于x轴对称的两点，直线 $\text{[math]}$ 、 $\text{[math]}$ 与曲线C分别交于点A、B（不与 $\text{[math]}$ 、 $\text{[math]}$ 重合），证明：直线AB过定点．
答案解析收藏纠错 + 选题