 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C . 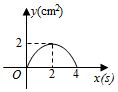 D .
D . 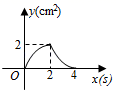

①作绕点A顺时针旋转一定角度后,顶点仍在格点上的
;
②请直接写出:点到
的距离为 ▲ .


人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
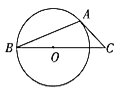
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.

如图②,AB与⊙O相切于点A , 当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D , 在上任取一点E , 连接EC , ED , EA , 则∠CED=∠CAD.
任务: