一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
-
-
A . 向左平移 个单位长度
B . 向左平移
个单位长度
B . 向左平移 个单位长度
C . 向右平移
个单位长度
C . 向右平移 个单位长度
D . 向右平移
个单位长度
D . 向右平移 个单位长度
个单位长度
-
-
-
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
A .  B .
B .  为偶函数
C .
为偶函数
C .  为单调递增函数
D .
为单调递增函数
D .  的值域为
的值域为
-
-
-
A . 若 , 则
, 则 B . 若点
B . 若点 在曲线
在曲线 上,则
上,则 C . 存在点
C . 存在点 , 使得曲线
, 使得曲线 与
与 关于点
关于点 对称
D . 方程
对称
D . 方程 恰有9个相异实数解
恰有9个相异实数解
三、填空题:本题共4小题,每小题5分,共20分.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程和演算步骤.
-
-
(1)

;
-
(2)

.
-
-
(1)
若

, 求

;
-
(2)
若

, 求实数

的取值范围.
-
-
-
(2)
若

, 求

的值.
-
20.
(2024高一上·南山期末)
已知某产品在过去的32天内的日销售量

(单位:万件)与第

天之间的函数关系为①

;②

这两种函数模型中的一个,且部分数据如下表:
 (天) (天)
| 2 | 4 | 10 | 20 |
 (万件) (万件)
| 12 | 11 | 10.4 | 10.2 |
-
(1)
请确定

的解析式,并说明理由;
-
(2)
若第

天的每件产品的销售价格均为

(单位:元),且

, 求该产品在过去32天内的第

天的销售额

(单位:万元)的解析式及

的最小值.
-
-
(1)
求

的解析式;
-
(2)
设

, 记

在区间

上的最大值为

, 求

的解析式.
-
-
(1)
求实数

的值;
-
(2)
(i)证明:

为单调递增函数;
(ii) , 若不等式
, 若不等式 恒成立,求非零实数
恒成立,求非零实数 的取值范围.
的取值范围.
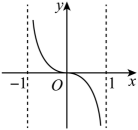 B .
B . 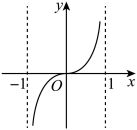 C .
C . 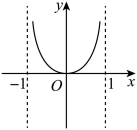 D .
D . 
, 若不等式
恒成立,求非零实数
的取值范围.