广东省江门市蓬江区怡福中学2023-2024学年九年级上册1...

更新时间：2024-03-21 浏览次数：19 类型：月考试卷

一、选择题（本大题共10小题，每小题3分，共30分）

1. (2023九上·蓬江月考) 下列图案代表四个城市的地铁标志，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·蓬江月考) 将函数 $\text{[math]}$ 的图象向右平移2个单位，再向上平移4个单位，可得到的抛物线的解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·蓬江月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在双曲线 $\text{[math]}$ 上，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023九上·蓬江月考) 如图， $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ 的度数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·蓬江月考) 下列事件中，是随机事件的是（）

A . 明天下雨 B . 15个人中至少有两个人出生在同月 C . 三角形内角和为180° D . 太阳从西方升起

答案解析收藏纠错 + 选题
6. (2023九上·蓬江月考) 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，以点A为圆心， $\text{[math]}$ 长为半径作 $\text{[math]}$ ，则原点O与 $\text{[math]}$ 的位置关系是（）

A . 点O在 $\text{[math]}$ 上 B . 点O在 $\text{[math]}$ 外 C . 点O在 $\text{[math]}$ 内 D . 以上皆有可能

答案解析收藏纠错 + 选题
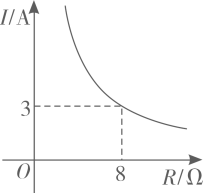
7. (2023九上·蓬江月考) 已知蓄电池的电压为定值，使用某蓄电池时，电流I(单位：A)与电阻R(单位： $\text{[math]}$ )是反比例函数关系，它的图象如图所示，则当电阻为 $\text{[math]}$ 时，电流为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·蓬江月考) 在一个不透明的袋子中，装有红色、黑色、白色的玻璃球共有40个，除颜色外其它都相同．若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在 $\text{[math]}$ 和 $\text{[math]}$ ，则该袋子中的白色球可能有（）

A . 6个 B . 16个 C . 18个 D . 24个

答案解析收藏纠错 + 选题
9. (2023九上·蓬江月考) 若关于x的一元二次方程 $\text{[math]}$ 的常数项为0，则m＝（）

A . 1 B . 2 C . 1或2 D . 0

答案解析收藏纠错 + 选题
10. (2023九上·蓬江月考) 二次函数 $\text{[math]}$ (a ， b ， c是常数， $\text{[math]}$ )的自变量x与函数值y的部分对应值如下表：
$\text{[math]}$
…
$\text{[math]}$
$\text{[math]}$
0
1
2
…
$\text{[math]}$
…
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
…
且当 $\text{[math]}$ 时，其对应的函数值 $\text{[math]}$ ．有下列结论：① $\text{[math]}$ ；②对称轴为 $\text{[math]}$ ；③ $\text{[math]}$ 和3是关于x的方程 $\text{[math]}$ 的两个根；④ $\text{[math]}$ 其中，正确结论的个数是（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题3分，共15分）

11. (2024八下·碑林月考) 点A（1，-5）关于原点的对称点为点B，则点B的坐标为．

答案解析收藏纠错 + 选题
12. (2024九上·楚雄期末) 如图，点A在反比例函数y＝ $\text{[math]}$ （x＞0）的图象上，过点A作AB⊥x轴于点B ，若△OAB的面积为3，则k＝．

答案解析收藏纠错 + 选题
13. (2023九上·蓬江月考) 现有一个圆心角为 $\text{[math]}$ ，半径为6cm的扇形纸片，用它恰好围成一个圆锥的侧面，该圆锥底面圆的半径为cm．

答案解析收藏纠错 + 选题
14. (2023九上·蓬江月考) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的解是 $\text{[math]}$ ，则 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
15. (2023九上·蓬江月考) 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 是正方形，点A的坐标为 $\text{[math]}$ ， $\text{[math]}$ 是以点B为圆心， $\text{[math]}$ 为半径的圆弧； $\text{[math]}$ 是以点O为圆心， $\text{[math]}$ 为半径的圆弧， $\text{[math]}$ 是以点C为圆心， $\text{[math]}$ 为半径的圆弧， $\text{[math]}$ 是以点A为圆心， $\text{[math]}$ 为半径的圆弧，继续以点B ， O ， C ， A为圆心按上述作法得到的曲线 $\text{[math]}$ 称为正方形的“渐开线”，则点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题

三、解答题（一）：本大题共3小题，第16题10分，17，18题每题7分，共24分．

16. (2023九上·蓬江月考)
1. （1）解方程： $\text{[math]}$ ．
2. （2）一个扇形的半径为4，扇形的弧长为 $\text{[math]}$ ，求扇形的圆心角的度数．
答案解析收藏纠错 + 选题
17. (2023九上·蓬江月考) 实施“双减”政策后，某校每周举行一次学科实践作业秀活动，内容有布艺、剪纸、卡通画（分别用A，B，C依次表示这三种作业）．小聪和小明计划每人选择一种作业，上述三种作业中的每一种作业被选中的可能性均相同．请你用列表法或画树状图法，求小聪和小明选择同一种作业的概率．

答案解析收藏纠错 + 选题
18. (2023九上·蓬江月考) 如图，利用一面墙（墙长20米），用总长43米的篱笆（图中实线部分）围成一个矩形鸡舍 $\text{[math]}$ ，且中间共留两个1米的小门．设篱笆 $\text{[math]}$ 长为x米．
1. （1） $\text{[math]}$ 米（用含x的代数式表示）；
2. （2）矩形鸡舍 $\text{[math]}$ 的面积的最大值是多少？说明理由．
答案解析收藏纠错 + 选题

四、解答题（二）：本大题共3小题，每小题9分，共27分．

19. (2023九上·蓬江月考) 某种原料需要达到 $\text{[math]}$ 及以上才能加工制作零件，如图表示原料的温度 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的关系，其中线段 $\text{[math]}$ 表示原料加热阶段；线段 $\text{[math]}$ 轴，表示原料的恒温阶段；曲线 $\text{[math]}$ 是双曲线 $\text{[math]}$ 的一部分，表示原料的降温阶段．根据图象回答下列问题：
1. （1）填空： $\text{[math]}$ 的值为；
2. （2）求线段 $\text{[math]}$ 对应的函数解析式；
3. （3）在图中所示的温度变化过程中，求可进行零件加工的时间长度．
答案解析收藏纠错 + 选题
20. (2023九上·蓬江月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）尺规作图：作 $\text{[math]}$ 的外接圆（保留作图痕迹）
2. （2）求（1）中所作外接圆的半径 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023九上·蓬江月考) 如图，把矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG，使点E落在对角线BD上，连接DG，DF.
1. （1）若∠BAE＝50°，求∠DGF的度数；
2. （2）求证：DF＝DC.
答案解析收藏纠错 + 选题

五、解答题（三）：本大题共2小题，每小题12分，共24分．

22. (2023九上·蓬江月考) 如图，⊙O是直角三角形ABC的外接圆，直径AC＝4，过C点作⊙O的切线，与AB延长线交于点D，M为CD的中点，连接BM，OM，且BC与OM相交于点N．
1. （1）求证：BM与⊙O相切；
2. （2）当∠BAC＝60°时，求弦AB和弧AB所夹图形的面积；
3. （3）在（2）的条件下，在弧AB上取一点F，使∠ABF＝15°，连接OF交弦AB于点H，求FH的长度是多少？
答案解析收藏纠错 + 选题
23. (2023九上·蓬江月考) 如图，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 和点B ，与y轴交于点 $\text{[math]}$ ，顶点为D ，连接 $\text{[math]}$ ， P是第一象限内抛物线上的动点，连接 $\text{[math]}$ ，设点P的横坐标为t ．
1. （1）求抛物线的解析式；
2. （2）当t为何值时， $\text{[math]}$ 的面积最大？并求出最大面积；
3. （3） M为直线 $\text{[math]}$ 上一点，求 $\text{[math]}$ 的最小值；
4. （4）过P点作 $\text{[math]}$ 轴，交 $\text{[math]}$ 于E点．是否存在点P ，使得 $\text{[math]}$ 为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

广东省江门市蓬江区怡福中学2023-2024学年九年级上册1...

副标题：

*注意事项：

广东省江门市蓬江区怡福中学2023-2024学年九年级上册1...

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	0	1	2	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…