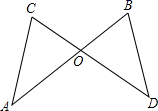
一、选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的。
-
-
-
-
-
5.
(2023八上·翁源月考)
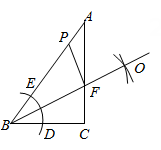
如图,在Rt

中,

, 利用尺规在

上分别截取

, 使

;分别以

为圆心,以大于

的长为半径作圆弧,两弧交于点

;作射线

交

于点

. 若

, 点

是

上的动点,则

的最小值为( )
A . 1
B . 2
C .  D . 无法确定
D . 无法确定
-
-
-
-
9.
(2023八上·翁源月考)
平面直角坐标系中,已知
A(2,0),
B(0,2)若在坐标轴上取
C点,使△
ABC为等腰三角形,则满足条件的点
C的个数是( )
A . 4
B . 6
C . 7
D . 8
-
10.
(2023八上·翁源月考)
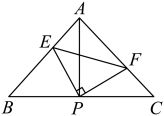
如图,已知在

中,

,

, 直角

的顶点P是

的中点,两边

、

分别交

、

于点E、F.以下四个结论:①

;②

是等腰直角三角形;③

;④

.其中正确的是( )
A . ①②③
B . ①②④
C . ②③④
D . ①②③④
二、填空题:本大题共6小题,每小题3分,共18分。
-
-
-
-
-
15.
(2023八上·翁源月考)
如图,小明与小红玩跷跷板游戏,已知跷跷板的支点

(即跷跷板的中点)至地面的距离是

, 当小红从水平位置

下降

时,这时小明离地面的高度是

.

-
三、解答题:本大题共9小题,共72分,解答要求写出文字说明、证明过程或演算步骤。
-
17.
(2023八上·翁源月考)
如图,在长度为1个单位长度的小正方形组成的正方形网格中,

的三个顶点

都在格点上.在图中画出与

关于

轴成轴对称的

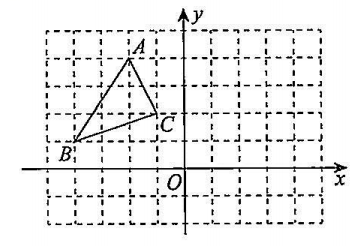
-
-
-
-
(1)
用尺规作图方法作

的垂直平分线

, 交

于点

, 交

于点

, 连接

. (保留作图痕迹,不写作法)
-
(2)
若

周长为13,求

的周长.
-
-
(1)
若

, 求

的度数.
-
(2)
当
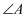
为多少度时,

?
-
-
-
-
(2)
如图②,当D点不在

的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由.
-
-
(1)
如图1,用两种不同的方法计算阴影部分的面积,可以得到的数学等式是.
-
(2)
我们可以利用(1)中的关系进行求值,例如,若

满足

, 可设

,

, 则

. 则

.
-
(3)
如图3,已知正方形

的边长为

分别是

上的点,且

, 长方形

的面积是24,分别以

为边作正方形,求阴影部分的面积.
-
-
(1)
如图1,若点

的横坐标为5,求点

的坐标;
-
(2)
如图2,若

轴恰好平分

交

轴于点

, 过点

作

轴于点

, 求

的值;
-
(3)
如图3,若点

的坐标为

, 点

在

轴的正半轴上运动时,分别以

为边在第一、第二象限作等腰

、等腰

, 连接

交

轴于点

, 当点

在

轴的正半轴上移动时,直接写出

的值.
 B .
B .  C .
C .  D .
D .