一、选择题(本大题10小题,每小题3分,共30分,在每小题的四个选项中,只有一项正确)
-
1.
(2023七上·南海月考)
如图,检测4个排球,其中质量超过标准的克数记为正数,不足的克数记为负数,从轻重的角度,下列最接近标准的是( )

-
2.
(2023七上·南海月考)
截至2022年底,深圳市注册志愿者已达3510000人,平均每5个深圳市民里就有一个志愿者.其中数据用科学记数法表示为( )
-
-
A . 调查某校七年级一班学生的课余体育运动情况
B . 调查某班学生早餐是否有喝牛奶的习惯
C . 调查某种 灯泡的质量
D . 调查某校篮球队员的身高
灯泡的质量
D . 调查某校篮球队员的身高
-
-
-
7.
(2023七上·南海月考)
如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )

A . 两点之间,线段最短
B . 两点确定一条直线
C . 过一点,有无数条直线
D . 连接两点之间的线段叫做两点间的距离
-
8.
(2023七上·南海月考)
如图,方格纸上每个小正方形的边长都相同,若使阴影部分能折叠成一个正方体,则需剪掉的一个小正方形不可以是( )
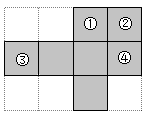
A . ①
B . ②
C . ③
D . ④
-
9.
(2023七上·南海月考)
在学习了《整式的及其加减》后,小龚同学总结出了一下结论,①0是最小的有理数;②字母

表示一个有理数,则

一定是负数:③若有理数

, 则数轴上表示

的点一定在表示

的点的右边:④一个数的平方为16,则这个数一定是4,其中正确的个数有( )
A . 1个
B . 2个
C . 3个
D . 4个
-
A . 168
B . 169
C . 195
D . 196
二、填空题:本大题6小题,每小题3分,共18分
-
-
-
13.
(2023七上·南海月考)
学情调查后,王老师将七年级1400名学生的数学成绩进行分类统计,得到如图所示的扇形统计图,则该年级有
名学生数学成绩为优.

-
-
15.
(2023七上·南海月考)
零陵楼是零陵古城的标志性建筑,如图,零陵楼下的桥洞是由一个半圆和一个长方形组成.若桥洞宽为

, 桥墩高为

, 则桥洞横截面的面积

.(用含

的代数式表示)

-
16.
(2024七上·旺苍期末)
如图,点

、

是线段

上两点,

、

分别是线段

、

的中点,给出下列结论:①若

, 则

;②

;则

;③

;其中正确的有
(请填写序号)

三、解答题一:(本大题4小题,第17、18题每小题4分,第19、20题每小题6分,共20分)
-
-
18.
(2023七上·南海月考)
小明和小亮利用温差来测量山峰的高度,小亮在山脚测得的温度是

, 此时小明在山顶测得的温度是

, 已知该地区高度每上升

, 气温下降

, 求这个山峰的高度.
-
-
(1)
画直线

;射线

;
-
(2)
在四边形

内找一点

, 使它到四边形四个顶点的距离的和

最小.
-
-
(1)
请在指定位置画出该几何体从左面、上面看到的形状图;
-
(2)
若从该几何体中移走一个小立方块,所得新几何体与原几何体相比,从左面、上面看到的形状图保持不变,请画出新几何体从正面看到的形状图.(一种即可)
四、解答题二:(本大题3小题,第21题每小题8分,第22、23题每小题10分,共28分)
-
-
22.
(2023七上·南海月考)
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量

(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表.
“宇宙2号”番茄挂果数量

-
(1)
统计表中,

,

;
-
-
(3)
若所种植的“宇番2号”番茄有1800株,请你估计挂果数量在55个以上(包含55个)有多少株?
-
-
(1)
作线段

, 使

;若

为

的中点,点

为

的中点,请在图中表示出来.
-
-
(3)
在(1)条件下,若

为

的中点,请求出

与

的数量关系.
五、解答题三;(本大题2小题,第24、25题每小题12分,共24分)
-
24.
(2023七上·南海月考)
当你记不住九九乘法表中乘9的口诀是,你可以进行如下的操作:例如,伸出两只手,做运算

时,如图,从左手开始数4下,数到第4根手指向下弯.这时,如图1该手指左边有3根手指,右边有6根手指,可得36,即

. 类似的,做运算

时,从左手开始数8下,数到第8根手指向下弯,这时,该手指左边有7根手指,右边有2根手指,可得72,即

.


-
(1)
在计算

时,从左手开始数,数到第
根手指向下弯下,这时,该手指左边有
根手指,右边有
根手指;
-
(2)
将问题一般化,我们可以解决

(

, 且

为整数)的问题.从左手开始数

下,数到第

根手指向下弯,此时该手指左边有
根手指,右边有
根手指,由此即可得

;
-
(3)
小郭同学在研究的过程中发现,若

是一个特殊两位数时,如

等,当这样的两位数与9相乘时,也能够通过指算法求解.如图2是

的指算法过程,假设

是这个两位数的个位数字,请用含有

的等式表示上述规律,并说明它的正确性.
-
-
-
(2)
动点

从点

出发,以

个单位

秒的速度向右运动,设运动时间为

秒,问:是否存在某个时刻

, 恰好使得

到点

的距离是点

到点

的距离的

倍?若存在,请求出

的值;若不存在,请说明理由
-
(3)
如图2在数轴上的点

和点

处各竖立一个挡板

点

在原点左侧,点

在原点右侧

, 数轴上甲、乙两个弹珠同时从原点出发,甲弹珠以

个单位

秒的速度沿数轴向左运动,乙弹珠以

个单位

秒的速度沿数轴向右运动.当弹珠遇到挡板后立即以原速度向反方向运动,若甲、乙两个弹珠相遇的位置恰好到点

和点

的距离相等.试探究点

对应的数与点

对应的数是否满足某种数量关系,请写出它们的关系式,并说明理由.

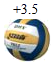 B .
B .  C .
C . 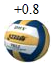 D .
D . 
![]()
 B .
B .  C .
C .  D .
D . 





