题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川省广安市岳池县2023-2024学年七年级上学期期末数学...

更新时间：2024-03-29 浏览次数：62 类型：期末考试

一、选择题（本大题共10小题，每小题3分，共30分。在每小题只有一个选项符合题意，请将所选选项填涂在答题卡上）

1. (2024七上·岳池期末) $\text{[math]}$ 绝对值是（）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七上·岳池期末) 围成下列立体图形的各个面中，只有平的面的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024七上·岳池期末) 若方程 $\text{[math]}$ 的解为 $\text{[math]}$ ，则式子 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
4. (2024七上·岳池期末) 2023年11月17日，备受瞩目的以“川渝韵味·香约广安”为城市主题的第六届世界川菜大会落下帷幕．据不完全统计，中国网对川菜大会和广安的直播浏览量达到155万人次，图文总阅读量达到1091.1万人次，直播观看总量达到98.9万人次．其中数据155万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七上·岳池期末) 如图，小军同学用剪刀沿虚线将一个长方形剪掉一角，发现剩下图形的周长比原长方形的周长小，能正确解释这一现象的数学知识是（）

A . 垂线段最短 B . 经过一点有无数条直线 C . 两点确定一条直线 D . 两点之间，线段最短

答案解析收藏纠错 + 选题
6. (2024七上·岳池期末) 有理数a ， b在数轴上的对应点的位置如图所示，则化简： $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七上·岳池期末) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七上·岳池期末) 我国古代数学问题：以绳测井，若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．绳长、井深各几何？这段话的意思是：用绳子量井深，把绳子三折来量，井外余绳四尺；把绳子四折来量，井外余绳一尺．绳长、井深各几尺？若设井深为x尺，根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024七上·岳池期末) 如图，已知线段AB的长为 $\text{[math]}$ ， C是线段AB的中点，若N是线段AC的三等分点，则线段BN的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
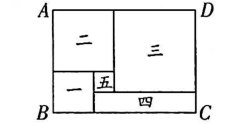
10. (2024七上·岳池期末) 如图，大长方形ABCD是由正方形一、二、三、五和小长方形四拼成的，且正方形一、二、三的边长分别为a ， b ， c（ $\text{[math]}$ ），有以下结论：① $\text{[math]}$ ；②小长方形四的宽是 $\text{[math]}$ ；③ $\text{[math]}$ ；④大长方形ABCD的周长为 $\text{[math]}$ 其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分。请将最简答案填写在答题卡相应位置）

11. (2024七上·岳池期末) 列式表示：比a的2倍小1的数是．

答案解析收藏纠错 + 选题
12. (2024七上·岳池期末) 比较大小： $\text{[math]}$ $\text{[math]}$ （填“>”或“<”）

答案解析收藏纠错 + 选题
13. (2024七上·岳池期末) 若单项式 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，则ab的值为．

答案解析收藏纠错 + 选题
14. (2024七上·岳池期末) 如图，有海岛A ， B ，已知海岛A在灯塔O北偏东 $\text{[math]}$ （ $\text{[math]}$ ）方向上，若 $\text{[math]}$ 与 $\text{[math]}$ 互余，则海岛B在灯塔O北偏西方向上．（角度用“度、分”表示）

答案解析收藏纠错 + 选题
15. (2024七上·岳池期末) 用“※”定义一种新运算：对于任意有理数x和y ，有 $\text{[math]}$ （a为常数），例如： $\text{[math]}$ ．若 $\text{[math]}$ 的值为 $\text{[math]}$ ，则a的值为．

答案解析收藏纠错 + 选题
16. (2024七上·岳池期末) 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第1次将点A向左移动3个单位长度到达点 $\text{[math]}$ ，第2次将点 $\text{[math]}$ 向右平移6个单位长度到达点 $\text{[math]}$ ，第3次将点 $\text{[math]}$ 向左移动9个单位长度到达点 $\text{[math]}$ ， …，按照这种规律移动下去，至少移动次后该点到原点O的距离不小于41．

答案解析收藏纠错 + 选题

三、解答题（本大题共4小题，第17小题5分，第18、19、20小题各6分，共23分）

17. (2024七上·岳池期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024七上·岳池期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024七上·岳池期末) 如图，已知线段AB ， a ， b ．
1. （1）请用尺规按下列要求作图：（不要求写作法，但要保留作图痕迹）
  ①延长线段AB ，在延长线上取点C，使 $\text{[math]}$ ；
  ②反向延长线段AB到点D，使 $\text{[math]}$ ．
2. （2）在（1）的条件下，如果 $\text{[math]}$ ，且E为CD的中点，求线段AE的长度
答案解析收藏纠错 + 选题
20. (2024七上·岳池期末) 已知关于x的一元一次方程 $\text{[math]}$ ，其中m是正整数．
1. （1）当 $\text{[math]}$ 时，解这个方程；
2. （2）若该方程有正整数解，求m的值
答案解析收藏纠错 + 选题

四、实践应用题（本大题共4小题，第21小题6分，第22、23、24小题各8分，共30分）

21. (2024七上·岳池期末) 如图是一个几何体的表面展开图．
1. （1）该几何体的名称是；
2. （2）将该展开图还原成几何体，若相对的两个面上的数互为相反数，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
22. (2024七上·岳池期末) 现代营养学家用身体质量指数衡量人体胖瘦程度，这个指数等于人体体重（ $\text{[math]}$ ）与人体身高（m）平方的商．对于成年人来说，身体质量指数低于18.5，体重过轻；身体质量指数在18.5~25范围内，体重适中；身体质量指数高于25，体重超重或肥胖．
1. （1）设一个人的体重为w（ $\text{[math]}$ ），身高为h（m），则他的身体质量指数p为．（用含w ， h的式子表示）
2. （2）李老师的身高是 $\text{[math]}$ ，体重是 $\text{[math]}$ ，他的体重是否适中？
答案解析收藏纠错 + 选题
23. (2024七上·岳池期末) 食品厂为检测某种袋装食品的质量是否符合标准（每袋以 $\text{[math]}$ 为标准质量），从该种袋装食品中抽出样品30袋，超过和不足标准质量的部分分别用正、负数表示，记录如下表：
与标准质量的差值/g
$\text{[math]}$
$\text{[math]}$
0
1
2
3
袋数
3
4
6
8
6
3
1. （1）若食品袋上标有“净重 $\text{[math]}$ ”，则这批样品中共有袋质量合格。
2. （2）这批样品平均每袋的质量比标准质量多（或少）多少克？
答案解析收藏纠错 + 选题

24. (2024七上·岳池期末) 元旦期间，某商场搞促销活动，具体内容如下表所示：

优惠条件

一次性购物不超过200元

一次性购物超过200元，但不超过500元

一次性购物超过500元

优惠方式

没有优惠

全部按九折优惠

其中500元仍按九折优惠；

超过500元的部分按八折优惠

（1）设一次性购买的物品原价是x元，当原价x超过200元但不超过500元时，实际付款为元；当原价x超过500元时，实际付款为元．（用含x的式子表示）
（2）若顾客甲购物时一次性付款490元，则甲所购物品的原价是多少元？

答案解析收藏纠错 + 选题

五、推理论证题（9分）

25. (2024七上·岳池期末) 如图，O是直线AB上的一点， $\text{[math]}$ ， OE是 $\text{[math]}$ 的平分线．
1. （1）如图1，当点C ， D ， E在直线AB的同侧时．
  ①若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
  ②若 $\text{[math]}$ ，则 $\text{[math]}$ ▲ ．（用含 $\text{[math]}$ 的式子表示）
2. （2）如图2，当点C与点D ， E在直线AB的两侧时，若 $\text{[math]}$ ，（1）中②的结论是否仍然成立？请给出你的结论，并说明理由．
答案解析收藏纠错 + 选题

六、拓展探究题（10分）

26. (2024七上·岳池期末) 【阅读】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了很多重要的规律：比如数轴上点A ， B分别表示有理数a ， b ，则A ， B两点之间的距离 $\text{[math]}$ ；线段AB的中，点P表示的数为 $\text{[math]}$ ．
【探究】如图，已知数轴上点A ， B分别表示数 $\text{[math]}$ ， 10，点M从点A出发，以每秒3个单位长度的速度向点B运动，同时点N从点B出发，以每秒2个单位长度的速度向点A运动．当点M ， N第一次相遇时，两点停止运动，设运动时间为t秒，线段MN的中点为P ．
1. （1）线段AB的中点表示的数为．
2. （2）求点P表示的数．（用含t的式子表示）
3. （3）若点M ， N第一次相遇后，继续以原来的速度和方向运动，点M到达点B后停留7秒，随后立即以原来的速度返回，点N到达点A后立即以原来的速度返回，两点再次相遇时，停止运动．在整个运动过程中，当 $\text{[math]}$ 时，求t的值．
答案解析收藏纠错 + 选题

试卷信息