 B .
B .  C .
C .  D .
D . 



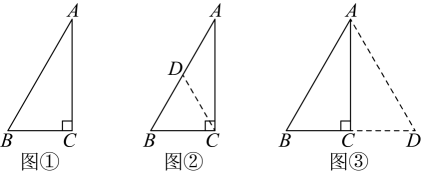
【证明】如图 , 在
中,
,
. 求证:
.
方法一:如图 , 作斜边
上的中线
, 则
.
,
.
是 ▲ 三角形.
.
方法二:如图 , 作点
关于
的对称点
, 连接
.
,
,
.
是等边三角形.
▲ .
.
①若 , 点
到边
的距离为 ▲ .
②若 , 求点
到边
的距离.
①求 的长(用含t的代数式表示)
②在点P运动的同时,作点B关于点N的对称点Q , 连结 .当
为等腰三角形时,直接写出t的值.