浙江省温州市名校2023-2024学年高三上学期数学1月第一...

更新时间：2024-04-04 浏览次数：63 类型：高考模拟

一、选择题：本大题共8小题，解小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高三上·温州模拟) 已知 $\text{[math]}$ 为虚数单位，则复数 $\text{[math]}$ 的虚部为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . 1

答案解析收藏纠错 + 选题
2. (2024高三上·温州模拟) 某校高一年级18个班参加艺术节合唱比赛，通过简单随机抽样，获得了10个班的比赛得分如下：91，89，90，92，94，87，93，96，91，85，则这组数据的80%分位数为（）

A . 93 B . 93.5 C . 94 D . 94.5

答案解析收藏纠错 + 选题
3. (2024高三上·温州模拟) 已知直线 $\text{[math]}$ 与圆 $\text{[math]}$ 有公共点，则b的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高三上·温州模拟) 三棱锥 $\text{[math]}$ 中， $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ 为等边三角形，且 $\text{[math]}$ ， $\text{[math]}$ ，则该三棱锥外接球的表面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高三上·温州模拟) 已知等比数列 $\text{[math]}$ 的首项 $\text{[math]}$ ，公比为q ，记 $\text{[math]}$ （ $\text{[math]}$ ），则“ $\text{[math]}$ ”是“数列 $\text{[math]}$ 为递减数列”的（）

A . 充要条件 B . 充分不必要条件 C . 必要不充分条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
6. (2024高一上·湖南期末) 已知函数 $\text{[math]}$ ，其中 $\text{[math]}$ .若 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
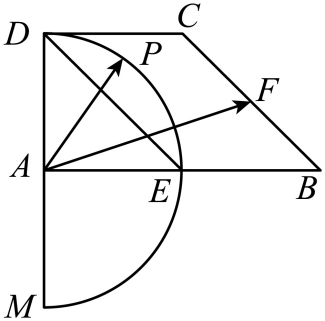
7. (2024高三上·温州模拟) 在直角梯形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ ， $\text{[math]}$ 的中点，点 $\text{[math]}$ 在以A为圆心， $\text{[math]}$ 为半径的圆弧 $\text{[math]}$ 上变动（如图所示），若 $\text{[math]}$ ，其中 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高三上·邵阳模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2024高三上·温州模拟) 下列选项中，与“ $\text{[math]}$ ”互为充要条件的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二下·广东期末) 设A ， B是一次随机试验中的两个事件，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . A ， B相互独立 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高三上·温州模拟) 在三棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是棱 $\text{[math]}$ 的中点， $\text{[math]}$ 是棱 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ，则（）

A . $\text{[math]}$ 平面 $\text{[math]}$ B . 平面 $\text{[math]}$ 平面 $\text{[math]}$ C . 点 $\text{[math]}$ 到底面 $\text{[math]}$ 的距离为2 D . 二面角 $\text{[math]}$ 的正弦值为 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高三上·温州模拟) 设 $\text{[math]}$ 为抛物线 $\text{[math]}$ 的焦点，直线 $\text{[math]}$ 与 $\text{[math]}$ 的准线 $\text{[math]}$ ，交于点 $\text{[math]}$ ．已知 $\text{[math]}$ 与 $\text{[math]}$ 相切，切点为 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 的一个交点为 $\text{[math]}$ ，则（）

A . 点 $\text{[math]}$ 在 $\text{[math]}$ 上 B . $\text{[math]}$ C . 以 $\text{[math]}$ 为直径的圆与 $\text{[math]}$ 相离 D . 直线 $\text{[math]}$ 与 $\text{[math]}$ 相切

答案解析收藏纠错 + 选题

三、填空题：本大题共4小题，每小题5分，共20分.

13. 已知 $\text{[math]}$ ， $\text{[math]}$ （a为实数）．若q的一个充分不必要条件是p ，则实数a的取值范围是.

答案解析收藏纠错 + 选题
14. (2024高三上·温州模拟) 已知正项数列 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2024高三上·温州模拟) 直三棱柱 $\text{[math]}$ 的底面是直角三角形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若平面 $\text{[math]}$ 将该直三棱柱 $\text{[math]}$ 截成两部分，将两部分几何体组成一个平行六面体，且该平行六面体内接于球，则此外接球表面积的最大值为．

答案解析收藏纠错 + 选题
16. (2024高三上·温州模拟) 对任意 $\text{[math]}$ ，函数 $\text{[math]}$ 恒成立，求a的取值范围．

答案解析收藏纠错 + 选题

四、解答题：木大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

17. (2024高三上·温州模拟) 在 $\text{[math]}$ 中，内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求角 $\text{[math]}$ 及边 $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
18. (2024高三上·温州模拟) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求数列 $\text{[math]}$ 的通项公式；
2. （2）若数列 $\text{[math]}$ 满足 $\text{[math]}$ ，其前 $\text{[math]}$ 项和为 $\text{[math]}$ ，求使得 $\text{[math]}$ 成立的 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
19. (2024高三上·温州模拟) 如图，正三棱锥 $\text{[math]}$ 的三条侧棱 $\text{[math]}$ 两两垂直，且长度均为2．E、F分别是 $\text{[math]}$ 的中点，H是 $\text{[math]}$ 的中点，过 $\text{[math]}$ 作平面与侧棱 $\text{[math]}$ 或其延长线分别相交于 $\text{[math]}$ ，已知 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题
20. (2024高三上·温州模拟) 甲、乙、丙为完全相同的三个不透明盒子，盒内均装有除颜色外完全相同的球.甲盒装有4个白球，8个黑球，乙盒装有1个白球，5个黑球，丙盒装有3个白球，3个黑球.
1. （1）随机抽取一个盒子，再从该盒子中随机摸出1个球，求摸出的球是黑球的概率；
2. （2）已知（1）中摸出的球是黑球，求此球属于乙箱子的概率.
答案解析收藏纠错 + 选题
21. (2024高三上·温州模拟) 设椭圆 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一个动点，点 $\text{[math]}$ ， $\text{[math]}$ 长的最小值为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值：
2. （2）设过点 $\text{[math]}$ 且斜率不为0的直线 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ 两点， $\text{[math]}$ 分别为 $\text{[math]}$ 的左、右顶点，直线 $\text{[math]}$ 和直线 $\text{[math]}$ 的斜率分别为 $\text{[math]}$ ，求证： $\text{[math]}$ 为定值．
答案解析收藏纠错 + 选题
22. (2024高三上·温州模拟) 已知 $\text{[math]}$ .
1. （1）若过点 $\text{[math]}$ 作曲线 $\text{[math]}$ 的切线，切线的斜率为2，求 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ 时，讨论函数 $\text{[math]}$ 的零点个数.
答案解析收藏纠错 + 选题