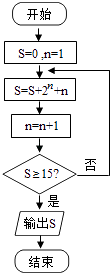
10.
(2014·福建理)
用a代表红球,b代表蓝球,c代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a)(1+b)的展开式1+a+b+ab表示出来,如:“1”表示一个球都不取、“a”表示取出一个红球,而“ab”则表示把红球和蓝球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的蓝球都取出或都不取出的所有取法的是( )
A . (1+a+a2+a3+a4+a5)(1+b5)(1+c)5
B . (1+a5)(1+b+b2+b3+b4+b5)(1+c)5
C . (1+a)5(1+b+b2+b3+b4+b5)(1+c5)
D . (1+a5)(1+b)5(1+c+c2+c3+c4+c5)
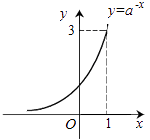 B .
B . 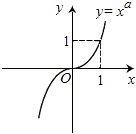 C .
C .  D .
D .