题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广西壮族自治区北海市2023-2024学年高一上学期期末教学...

更新时间：2024-03-07 浏览次数：13 类型：期末考试

一、､单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024高一下·富源月考) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一上·北海期末) 命题“ $\text{[math]}$ ”的否定为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一上·北海期末) 王明正在筹划班级迎新晚会，想知道该准备多少斤水果，他最希望得到所有学生需要水果数量的（）

A . 四分位数 B . 中位数 C . 众数 D . 均值

答案解析收藏纠错 + 选题
4. (2024高一上·北海期末) 函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024高一上·北海期末) 已知偶函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递增，且 $\text{[math]}$ ，则关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一上·北海期末) 已知 $\text{[math]}$ 且在 $\text{[math]}$ 内存在零点，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一上·北海期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一上·北海期末) 已知实数 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、､多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2024高一上·北海期末) 下列每组函数不是同一函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一上·北海期末) 今年“五一”假期，各大商业综合体､超市等纷纷抓住节日商机，积极开展各类促销活动.在某超市购买80元以上商品的顾客可以参加一次抽奖活动，若顾客小王中奖的概率为0.4，顾客小张中奖的概率为0.2，则（）

A . 小王和小张都中奖的概率为0.08 B . 小王和小张都没有中奖的概率为0.46 C . 小王和小张中只有一个人中奖的概率为0.44 D . 小王和小张中至多有一个人中奖的概率为0.92

答案解析收藏纠错 + 选题
11. (2024高一上·北海期末) 下列命题中正确的是（）

A . “ $\text{[math]}$ ”是“ $\text{[math]}$ ”的必要不充分条件 B . “ $\text{[math]}$ 且 $\text{[math]}$ ”是“ $\text{[math]}$ ”的充分不必要条件 C . “ $\text{[math]}$ ”是“ $\text{[math]}$ ”的充要条件 D . “ $\text{[math]}$ ”是“ $\text{[math]}$ ”的充要条件

答案解析收藏纠错 + 选题
12. (2024高一上·北海期末) 已知函数 $\text{[math]}$ .若互不相等的实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值可以是（）

A . -8 B . -7 C . -6 D . -5

答案解析收藏纠错 + 选题

三、､填空题：本题共4小题，每小题5分，共20分.

13. (2024高一上·北海期末) 某高中共有学生1000人，其中高一和高二各有400人，现采用按比例分配的分层抽样的方法抽取容量为25的样本，那么高二抽取的人数为.

答案解析收藏纠错 + 选题
14. (2024高一上·北海期末) 某公司在甲､乙两地销售同一种农产品，利润（单位：万元）分别为 $\text{[math]}$ ，其中 $\text{[math]}$ 为销售量（单位：吨）.若该公司在这两地共销售10吨农产品，则能获得的最大利润为万元.

答案解析收藏纠错 + 选题
15. (2024高一上·北海期末) 从分别写有 $\text{[math]}$ 的7张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数字大于第二卡片上的数字的概率为.

答案解析收藏纠错 + 选题
16. (2024高一上·北海期末) 若函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减，则实数 $\text{[math]}$ 的取值范围为.

答案解析收藏纠错 + 选题

四、､解答题：本题共6小题，共70分.解答应写出必要的文字说明､证明过程及演算步骤.

17. (2024高一上·北海期末) 设集合 $\text{[math]}$ .求：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高一上·北海期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2024高一上·北海期末) 已知函数 $\text{[math]}$ （ $\text{[math]}$ 且 $\text{[math]}$ ）．
1. （1）求关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集；
2. （2）若函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上的最大值和最小值之和为 $\text{[math]}$ ，求实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
20. (2024高一上·北海期末) 已知幂函数 $\text{[math]}$ 既不是奇函数，也不是偶函数.
1. （1）求 $\text{[math]}$ 的值；
2. （2）若函数 $\text{[math]}$ 的最小值为-3，求实数 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
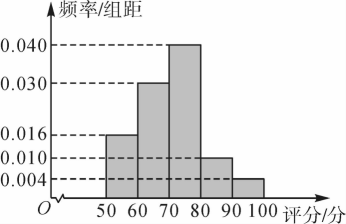
21. (2024高一上·北海期末) 居民小区物业服务联系着千家万户，关系着居民的“幸福指数”.某物业公司为了调查小区业主对物业服务的满意程度，以便更好地为业主服务，随机调查了100名业主，根据这100名业主对物业服务的满意程度给出评分，分成 $\text{[math]}$ 五组，得到如图所示的频率分布直方图.
1. （1）在这100名业主中，求评分在区间 $\text{[math]}$ 的人数与评分在区间 $\text{[math]}$ 的人数之差；
2. （2）估计业主对物业服务的满意程度给出评分的众数和 $\text{[math]}$ 分位数；
3. （3）若小区物业服务满意度（满意度 $\text{[math]}$ ）低于0.8，则物业公司需要对物业服务人员进行再培训.请根据你所学的统计知识，结合满意度，判断物业公司是否需要对物业服务人员进行再培训，并说明理由.（同一组中的数据用该区间的中点值作代表）
答案解析收藏纠错 + 选题
22. (2024高一上·北海期末) 已知函数 $\text{[math]}$ 是定义在 $\text{[math]}$ 上的奇函数.
1. （1）求实数 $\text{[math]}$ 的值；
2. （2）证明：函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递增；
3. （3）记 $\text{[math]}$ ，对 $\text{[math]}$ ，不等式 $\text{[math]}$ 恒成立，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

试卷信息