云南省大理白族自治州民族中学2023-2024学年高一下学期...

更新时间：2024-04-04 浏览次数：17 类型：月考试卷

一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. (2024高一下·大理月考) 在平面直角坐标系中，给出下列命题：①小于 $\text{[math]}$ 的角一定是锐角；②钝角一定是第二象限的角；③终边不重合的角一定不相等；④第二象限角大于第一象限角。
其中假命题的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
2. (2024高一下·大理月考) 若角 $\text{[math]}$ 的终边在直线 $\text{[math]}$ 上，则角 $\text{[math]}$ 的取值集合为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一下·大理月考) 若 $\text{[math]}$ 是第一象限角，则下列各角是第三象限角的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一下·大理月考) 设 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·大理月考) 若函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的图象经过定点 $\text{[math]}$ ，且点 $\text{[math]}$ 在角 $\text{[math]}$ 的终边上，则 $\text{[math]}$ 的值等于（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
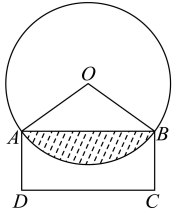
6. (2024高一下·大理月考) “圆材埋壁”是我国古代的数学著作《九章算术》中的一个问题，现有一个“圆材埋壁”模型，其截面如图所示．若圆柱材料的截面圆的半径长为1，圆心为 $\text{[math]}$ ，墙壁截面 $\text{[math]}$ 为矩形，且劣弧 $\text{[math]}$ 的长等于半径 $\text{[math]}$ 长的2倍，则圆材埋在墙壁内部的截面面积是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·大理月考) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一下·大理月考) 已知函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增，则实数a的最大值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. (2024高一下·大理月考) 关于函数 $\text{[math]}$ ，下面四个命题中是真命题的是（）

A . $\text{[math]}$ 的图像关于 $\text{[math]}$ 轴对称 B . $\text{[math]}$ 的图像关于原点对称 C . $\text{[math]}$ 的图像关于直线 $\text{[math]}$ 对称 D . $\text{[math]}$ 的最小值为2

答案解析收藏纠错 + 选题
10. (2024高一下·大理月考) 函数 $\text{[math]}$ 在其定义域上的图像是如图所示折线段 $\text{[math]}$ ，其中点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以下说法中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ 的解集为 $\text{[math]}$ C . $\text{[math]}$ 为偶函数 D . 若 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减，则 $\text{[math]}$ 的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一下·大理月考) 设函数 $\text{[math]}$ （ $\text{[math]}$ ），已知 $\text{[math]}$ 在 $\text{[math]}$ 上有且仅有5个零点，下述四个结论中结论正确的是（）

A . $\text{[math]}$ 在 $\text{[math]}$ 有且仅有3个最大值点 B . $\text{[math]}$ 在 $\text{[math]}$ 有且仅有2个最小值点 C . $\text{[math]}$ 在 $\text{[math]}$ 单调递增 D . $\text{[math]}$ 的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分．

12. (2024高一下·大理月考) 函数 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
13. (2024高一下·大理月考) 借助函数 $\text{[math]}$ 的图象，可知不等式 $\text{[math]}$ ， $\text{[math]}$ 的解集为．

答案解析收藏纠错 + 选题
14. (2024高一下·大理月考) 求值： $\text{[math]}$ .

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．

15. (2024高一下·上饶月考) 已知 $\text{[math]}$ ．
1. （1）化简 $\text{[math]}$ ；
2. （2）已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
16. (2024高一下·大理月考) 证明：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3）已知 $\text{[math]}$ ， $\text{[math]}$ ，求证 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024高一下·大理月考) 已知函数 $\text{[math]}$ 的最大值为1，
1. （1）求常数 $\text{[math]}$ 的值；
2. （2）求函数 $\text{[math]}$ 的单调递减区间；
3. （3）求使 $\text{[math]}$ 成立的 $\text{[math]}$ 的取值集合．
答案解析收藏纠错 + 选题
18. (2024高三上·上海市月考) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，（ $\text{[math]}$ ）
1. （1）当 $\text{[math]}$ 时，解不等式 $\text{[math]}$ ；
2. （2）若任意 $\text{[math]}$ ，都有 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围；
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ，使得不等式 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2024高一下·大理月考) 对于定义域为 $\text{[math]}$ 的函数，如果存在区间 $\text{[math]}$ ，同时满足下列两个条件：
① $\text{[math]}$ 在区间 $\text{[math]}$ 上是单调的；
②当定义域是 $\text{[math]}$ 时， $\text{[math]}$ 的值域也是 $\text{[math]}$ ．则称 $\text{[math]}$ 是函数 $\text{[math]}$ 的一个“黄金区间”．
1. （1）请证明：函数 $\text{[math]}$ 不存在“黄金区间”．
2. （2）已知函数 $\text{[math]}$ 在 $\text{[math]}$ 上存在“黄金区间”，请求出它的“黄金区间”．
3. （3）如果 $\text{[math]}$ 是函数 $\text{[math]}$ 的一个“黄金区间”，请求出 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题