一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
-
5.
(2024·深圳 高一上期末)
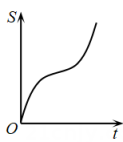
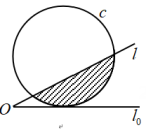
如图,直线和圆

, 当

从

开始在平面上绕点

按逆时针方向匀速转动(转动角度不超过

)时,它扫过的圆内阴影部分的面积

是时间

的函数,这个函数的图象大致是( )
-
A . 向右平移 个单位长度
B . 向右平移
个单位长度
B . 向右平移 个单位长度
C . 向左平移
个单位长度
C . 向左平移 个单位长度
D . 向左平移
个单位长度
D . 向左平移 个单位长度
个单位长度
-
-
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
A .  与g(x)=x
B . f(x)=2lnx与
与g(x)=x
B . f(x)=2lnx与 C .
C .  与
与 D .
D .  与
与
-
-
A .  的值域是
的值域是 B .
B .  的图象关于原点对称
C .
的图象关于原点对称
C .  在其定义域内单调递减
D . 方程
在其定义域内单调递减
D . 方程 有且仅有两根
有且仅有两根
-
A .  B . 若
B . 若 , 则
, 则 C .
C .  是偶函数
D .
是偶函数
D .  的取值范围是
的取值范围是
三、填空题:本大题共4小题,每小题5分,共20分.
-
-
-
15.
(2024·深圳 高一上期末)
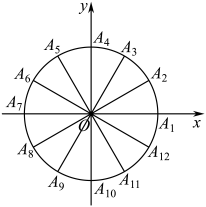
如图,单位圆被点

,

,

, …,

平均分成

份,以

轴的正半轴为始边,

(

…

)为终边的角记为

, 则

=
,

=
.(
说明:∑是一个连加符号,

…

)
-
四、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
-
(1)
计算:

;
-
-
-
(1)
求

的值;
-
(2)
当

时,求

的单调递增区间.
-
-
(1)
请在图中同一坐标系内画出函数

的图象.设

与

在

轴左边的交点为

, 试用二分法求出

的横坐标

的近似解(精确度为0.3);
-
(2)
用

表示

,

中的较大者,记为


, 请写出

的解析式.
-
-
(1)
若

, 求方程

的解;
-
-
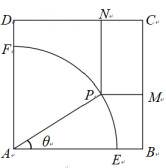
21.
(2024·深圳 高一上期末)
如图所示,某开发区有一块边长为


的正方形空地

. 当地政府计划将它改造成一个体育公园,在半径为


的扇形

上放置健身器材,并在剩余区域中修建一个矩形运动球场

, 其中
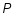
是弧

上一点,

分别在边BC、CD上.设

, 球场

的面积

.
-
(1)
求

的解析式;
-
(2)
若球场平均每平方米的造价为

元,问:当角

为多少时,球场的造价

最低.
-
22.
(2024·深圳 高一上期末)
若函数y=f(x)的定义域为(0,m),若对于给定的正实数n,存在0<x
0<m-n,使得f(x
0)=f(x
0+n),则称函数y=f(x)在(0,m)上具有性质P(n).
-
(1)
若函数f(x)=x+

在区间(0,m)上具有性质P(1),求正整数m的最小值;
-
(2)
若函数f(x)=sinπx在区间(0,2)上具有性质P(n),求n的取值范围.
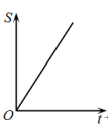 B .
B . 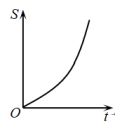 C .
C . 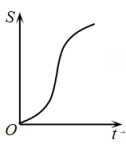 D .
D .