贵州省黔东南州从江县停洞中学2023-2024学年九年级下学...

更新时间：2024-07-31 浏览次数：20 类型：月考试卷

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2024九下·从江月考) 下列四组图形中，不是相似图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九下·从江月考) 已知2x=5y(y≠0)，则下列比例式成立的是（）

A . $\text{[math]}$ = $\text{[math]}$ B . $\text{[math]}$ = $\text{[math]}$ C . $\text{[math]}$ = $\text{[math]}$ D . $\text{[math]}$ = $\text{[math]}$

答案解析收藏纠错 + 选题
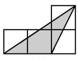
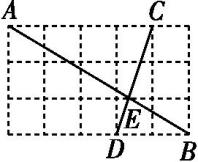
3. (2024九下·从江月考) 如图所示，在5×3的正方形网格中，每个小格的顶点叫做格点，点A，B，C，D都在格点上，线段AB与CD相交于点E，则 AE∶BE等于（）

A . 2∶1 B . 3∶1 C . 3∶2 D . 4∶1

答案解析收藏纠错 + 选题
4. (2024九下·从江月考) 如图所示，小正方形的边长均为1，则图中三角形(阴影部分)与△ABC相似的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
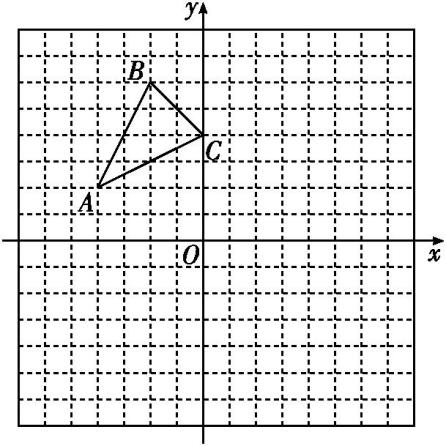
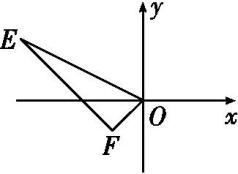
5. (2024九下·从江月考) 如图所示，在平面直角坐标系中，点 E(-4，2)，F(-1，-1)，以O为位似中心，按相似比为1∶2把△EFO缩小，则点E的对应点E′的坐标为（）

A . (2，-1)或(-2，1) B . (8，-4)或(-8，4) C . (2，-1) D . (8，-4)

答案解析收藏纠错 + 选题
6. (2024九下·从江月考) 如图所示，已知∠DAB=∠CAE，那么添加下列一个条件后，仍然无法判定△ABC∽△ADE的是（）

A . $\text{[math]}$ = $\text{[math]}$ B . $\text{[math]}$ = $\text{[math]}$ C . ∠B=∠D D . ∠C=∠AED

答案解析收藏纠错 + 选题
7. (2024九下·从江月考) 如图所示，以点O为位似中心，将△ABC放大得到△DEF.若AD=OA，则△ABC与△DEF的面积之比为a∶b，则 $\text{[math]}$ 等于（）

A . 1∶6 B . 1∶5 C . 1∶4 D . 1∶2

答案解析收藏纠错 + 选题
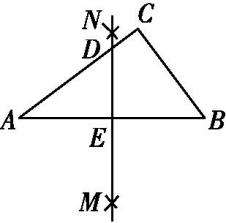
8. (2024九下·从江月考) 如图所示，在Rt△ABC中，∠C=90°，AB=5，BC=3，利用尺规作图：分别以点A，B为圆心，大于 $\text{[math]}$ AB的长为半径作弧，两弧交点分别为M，N.连接MN与AC交于点D，与AB交于点E，则DE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
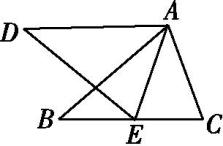
9. (2024九下·从江月考) 如图所示，D，E分别是△ABC的边AB，BC上的点，DE∥AC，若S_△_BDE∶S_△_CDE=1∶4，则S_△_BDE∶S_△_ADC的值为（）

A . 1∶16 B . 1∶18 C . 1∶20 D . 1∶24

答案解析收藏纠错 + 选题
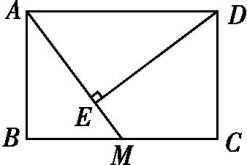
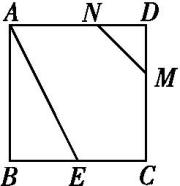
10. (2024九下·从江月考) 如图所示，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点分别在CD，AD上滑动.若要△ABE与以点D，点M，点N为顶点的三角形相似，则DM的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
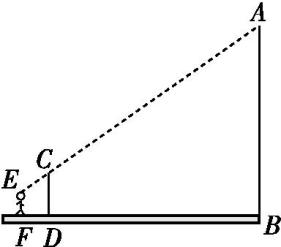
11. (2024九下·从江月考) 西周数学家商高总结了用“矩”[如图(1)所示]测量物高的方法：把矩的两边按图(2)放置，从“矩”CDA的一端A(人眼)望点E，使视线通过“矩”的另一端点C，记人站立的位置为点B，量出BG长，即可算得物高EG.若a=30 cm，b=60 cm，AB=1.6 m，BG=2.4 m，则EG的高度为（）

A . 1.2 m B . 2.8 m C . 4.8 m D . 6.4 m

答案解析收藏纠错 + 选题
12. (2024九下·从江月考) 如图所示，在△ABC中，AB=AC=4，BC=2 $\text{[math]}$ ，以AB为直径的☉O分别交AC，BC于点D，E，连接ED，则CD的长为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2024九下·从江月考) 已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2024九下·从江月考) 如图所示，△ABC和△DEF是以点O为位似中心的位似图形.若OA∶AD=2∶3，则△ABC与△DEF的周长比是.

答案解析收藏纠错 + 选题
15. (2024九下·从江月考) 如图所示的是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2 m，BP=1.8 m，PD=12 m，那么该古城墙的高度是m(平面镜的厚度忽略不计).

答案解析收藏纠错 + 选题
16. (2024九下·从江月考) 如图所示，在矩形ABCD中，AD=8，AE⊥BD，垂足为E，ED=4BE，则AE的长为.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2024九下·从江月考) 已知 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ≠0，求 $\text{[math]}$ 的值.

答案解析收藏纠错 + 选题
18. (2024九下·从江月考) 如图所示，在△ABC和△DEC中，∠A=∠D，∠BCE=∠ACD.
1. （1）求证：△ABC∽△DEC；
2. （2）若S_△_ABC∶S_△_DEC=4∶9，BC=6，求CE的长.
答案解析收藏纠错 + 选题
19. (2024九下·从江月考) 如图所示，已知A(-4，2)，B(-2，6)，C(0，4)是平面直角坐标系中的三点.
1. （1）把△ABC向右平移4个单位长度再向下平移1个单位长度，得到△A₁B₁C₁.画出平移后的图形，并写出点A的对应点A₁的坐标；
2. （2）以原点O为位似中心，将△ABC缩小为原来的一半，得到△A₂B₂C₂ ，请在所给的平面直角坐标系中作出所有满足条件的图形.
答案解析收藏纠错 + 选题
20. (2024九下·从江月考) 如图所示，四边形ABCD为菱形，点E在AC的延长线上，∠ACD=∠ABE.
1. （1）求证：△ABC∽△AEB；
2. （2）当AB=6，AC=4时，求AE的长.
答案解析收藏纠错 + 选题
21. (2024九下·从江月考) 如图所示，九年级(1)班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD=3 m，标杆与旗杆的水平距离BD=15 m，人的眼睛与地面的高度EF=1.6 m，人与标杆CD的水平距离DF=2 m，求旗杆AB的高度.

答案解析收藏纠错 + 选题
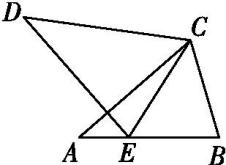
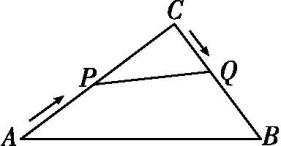
22. (2024九下·从江月考) 如图所示，点D在三角形ABC的边AB上，DE交AC于点E，∠ADE=∠B，点F在AD上，且AD²=AF·AB.求证：
1. （1） $\text{[math]}$ = $\text{[math]}$ ；
2. （2） △AEF∽△ACD.
答案解析收藏纠错 + 选题
23. (2024九下·从江月考) 如图所示，在矩形ABCD中，AB=2，BC=3，M是BC的中点，DE⊥AM于点E.
1. （1）求证：△ADE∽△MAB；
2. （2）求DE的长.
答案解析收藏纠错 + 选题
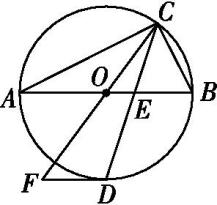
24. (2024九下·从江月考) 如图所示，点C在以AB为直径的☉O上，CD平分∠ACB交☉O于点D，交AB于点E，过点D作☉O的切线交CO的延长线于点F.
1. （1）求证：DF∥AB；
2. （2）若AC=2 $\text{[math]}$ ， BC= $\text{[math]}$ ，求FD的长.
答案解析收藏纠错 + 选题
25. (2024九下·从江月考) 如图所示，在 Rt△ABC 中，∠C=90°，AC=20 cm，BC=15 cm，现有动点P从点A出发，沿线段AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动.如果点P的速度是4 cm/s，点Q的速度是 2 cm/s，它们同时出发，当有一点到达所在线段的端点时，两点都停止运动.设运动时间为t.
1. （1）当t=3 s时，P，Q两点之间的距离是多少?
2. （2）若△CPQ的面积为S，求S关于t的函数解析式.
3. （3）当t为多少时，以点C，P，Q为顶点的三角形与△ABC相似?
答案解析收藏纠错 + 选题