一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.
-
1.
若∠A=40°,则∠A的补角为( )
A . 40°
B . 50°
C . 60°
D . 140°
-
2.
(2023七上·花溪月考)
如图所示,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( )
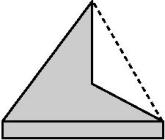
A . 两直线相交只有一个交点
B . 两点确定一条直线
C . 经过一点有无数条直线
D . 两点之间,线段最短
-
-
A . AC=AD-CD
B . AC=AB+BC
C . AC=BD-AB
D . AC=AD-AB
-
-
-
A . 正方体、圆柱、三棱柱、圆锥
B . 正方体、圆锥、三棱柱、圆柱
C . 正方体、圆柱、三棱锥、圆锥
D . 正方体、圆柱、四棱柱、圆锥
-
A . 150°
B . 145°
C . 140°
D . 135°
-
9.
(2023七上·花溪月考)
如图所示,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,若∠1=27°41
' , 则∠2的大小是( )
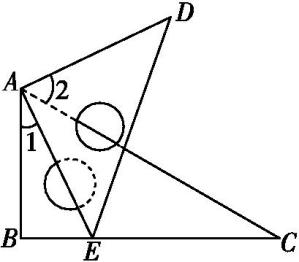
A . 27°41'
B . 57°41'
C . 58°19'
D . 32°19'
-
A . 60°
B . 70°
C . 75°
D . 80°
-
11.
(2023七上·花溪月考)
如图所示,C为线段AB的中点,AC=5,D在线段AB上,D是线段AB的三等分点,则BD的长是( )

-
12.
(2023七上·花溪月考)
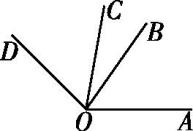
如图所示,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的有( )
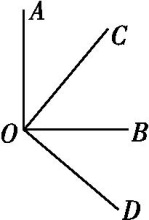
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题:本大题4小题,每小题4分,共16分.
-
-
-
15.
(2023七上·花溪月考)
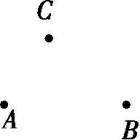
如图所示的是一个长方体的表面展开图,其中四边形ABCD是正方形,根据图中标注的数据可求得原长方体的体积是
.

-
16.
(2023七上·花溪月考)
如图所示,把一根绳子AB以中点O对折,点A和点B重合,折成一条线段OB,在线段OB上取一点P,使OP∶BP=1∶3,从P处把绳子剪断,得到三段绳子.若剪断后的三段绳子中最短的一段为 16 cm,则绳子的原长为
cm.

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
-
-
-
-
-
-
(3)
若点E在直线AB上,且EA=2 cm,求BE的长.
-
-
(1)
若∠AOC=60°,请求出∠AOD和∠BOC的度数;
-
(2)
若∠AOD和∠DOE互余,且∠AOD=

∠AOE,请求出∠AOD和∠COE的度数.
-
-
-
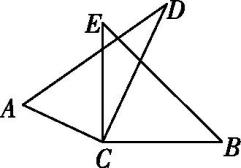
(2)
若∠ACB=144°42' , 则∠DCE的度数为;
-
(3)
猜想∠ACB与∠DCE的大小关系,并说明理由.
-
23.
(2023七上·花溪月考)
如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,则∠1,∠2互为垂角,即∠1是∠2的垂角(本题中的所有角都是指大于0°且小于180°的角).
-
(1)
∠α=54°,∠β=137°,求它们的垂角分别是多少度.
-
(2)
如果一个角的垂角等于这个角的补角的

, 求这个角的度数.
-
24.
(2023七上·花溪月考)
如图所示,点C在线段AB上,M是AC的中点,N是BC的中点,若 AC∶CB=3∶2,且MC+NB=12.5 cm,求MC的长.

-
25.
(2023七上·花溪月考)
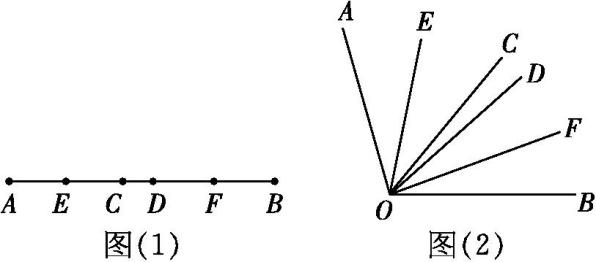
如图(1)所示,已知线段AB=18 cm,CD=2 cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.
-
-
(2)
当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变,请求出EF的长度,如果变化,请说明理由;
-
(3)
a.我们发现角的很多规律和线段一样,如图(2)所示,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD.若∠AOB=140°,∠COD=40°,求∠EOF.
b.由此,你猜想∠EOF,∠AOB和∠COD会有怎样的数量关系(直接写出猜想即可).

![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()


![]()
![]()

![]()
