一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
-
-
5.
(2024高一下·湘阴开学考)
函数

的一个正数零点附近的函数值用二分法逐次计算,参考数据如下:

,

,

,

,

,

, 那么方程的一个近似解(精确度为0.1)为( )
A . 1.5
B . 1.25
C . 1.41
D . 1.44
-
-
-
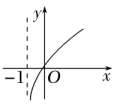
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求,全部选对得5分,选对但不全的得2分,有选错的不得分)
-
A .  ,
,  B .
B .  ,
,  为偶数
C . 所有菱形的四条边都相等
D .
为偶数
C . 所有菱形的四条边都相等
D .  是无理数
是无理数
-
-
-
A .  的最小正周期为
的最小正周期为 B . 对任意的
B . 对任意的 , 都有
, 都有 C .
C .  在
在 上是增函数
D . 由
上是增函数
D . 由 的图象向右平移
的图象向右平移 个单位长度得曲线
个单位长度得曲线
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
-
-
-
15.
(2024高一下·湘阴开学考)
Logistic模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数

(

单位:天)的Logistic模型:

, 其中

为最大确诊病例数.当

时,标志着已初步遏制疫情,则

约为
天.(注:

为自然对数的底数,

)
-
四、解答题(共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
-
(1)
若

, 求集合

;
-
(2)
若

, 求实数

的取值范围.
-
-
(1)
求

和

的值;
-
(2)
当

,

, 且满足

时,有

恒成立,求

的取值范围.
-
-
20.
(2024高一下·湘阴开学考)
已知某观光海域
AB段的长度为3百公里,一超级快艇在
AB段航行,经过多次试验得到其每小时航行费用
Q(单位:万元)与速度
v(单位:百公里/小时)(0≤
v≤3)的以下数据:
|
 | 0 | 1 | 2 | 3 |
|  | 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv , Q=0.5v+a , Q=klogav+b .
-
(1)
试从中确定最符合实际的函数模型,并求出相应的函数解析式;
-
(2)
该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
-
-
(1)
求

的解析式;
-
(2)
将函数

的图象上所有点的横坐标缩短到原来的

(纵坐标不变),再将所得函数图象向右平移

个单位长度,得到函数

的图象,求

的单调递增区间.
-
-
(1)
求

的值;
-
(2)
若函数

,

, 是否存在实数

使得

的最小值为0,若存在,求出

的值;若不存在,请说明理由.
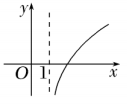 B .
B . 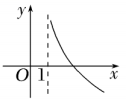 C .
C . 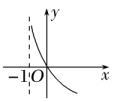 D .
D .