一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
A . A=B
B . B⊆A
C . A∈B
D . A⊆B
-
A .  是假命题
B .
是假命题
B .  :
: ,
,  C .
C .  是假命题
D .
是假命题
D .  :存在一个大于2的质数不是奇数
:存在一个大于2的质数不是奇数
-
-
A . “ ”是“
”是“ ”的充分不必要条件
B . “
”的充分不必要条件
B . “ ”是“
”是“ ”的必要不充分条件
C . “
”的必要不充分条件
C . “ ”是“
”是“ ”的充要条件
D . “
”的充要条件
D . “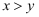 ”是“
”是“ ”的既不充分也不必要条件
”的既不充分也不必要条件
-
-
6.
(2024高一下·东坡开学考)
我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”现有一类似问题,不确定大小的圆柱形木材,部分埋在墙壁中,其截面如图所示.用锯去锯这木材,若锯口深

, 锯道

, 则图中

与弦

围成的弓形的面积为( )

-
A . 9
B . 10
C . 11
D . 12
-
8.
(2024高一下·东坡开学考)
已知定义在

上的函数

的图像连续不断,若存在常数

, 使得

对于任意的实数

恒成立,则称

是“回旋函数”.若函数

是“回旋函数”,且

, 则

在

上( )
A . 至多有2022个零点
B . 至多有1011个零点
C . 至少有2022个零点
D . 至少有1011个零点
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
-
-
-
A .  的最大值为
的最大值为 B .
B .  的最小值为4
C .
的最小值为4
C .  的最小值为
的最小值为 D .
D .  的最小值为16
的最小值为16
-
A .  是奇函数
B .
是奇函数
B .  在定义域上单调递增
C . 当
在定义域上单调递增
C . 当 时,函数
时,函数 D .
D . 
三、填空题:本大题共4小题,每小题5分,共20分。
四、解答题:本大题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。
-
-
-
-
(1)
化简

;
-
(2)
若

, 求

;
-
(3)
若

, 求

.
-
20.
(2024高一下·东坡开学考)
某城市规划部门为改善早晚高峰期间某条地下隧道的车辆通行能力,研究了该隧道内的车流速度
v(单位:千米/小时)和车流密度
x(单位:辆/千米)所满足的关系式

(
k单位:辆/小时).研究发现:当隧道内的车流密度达到120辆/千米时造成堵塞,此时车流速度是0千米小时.
-
(1)
若车流密度为50辆/千米.求此时的车流速度;
-
(2)
若车流速度v不小于40千米/小时.求车流密度x的取值范围.
-
-
(1)

;
-
(2)
求证:

在
R上为增函数;
-
(3)
若关于
x的不等式

对于任意

恒成立,求实数
t的取值范围.
-
-
(1)
求函数

,

的解析式;
-
(2)
若关于
x的不等式

在

上恒成立,求正实数
a的取值范围.
