广东省茂名市高州市2023-2024学年七年级上学期数学期末...

更新时间：2024-04-01 浏览次数：38 类型：期末考试

一、选择题:本大题共10小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项是符合题目要求的.

1. (2024七上·高州期末) 如果向东走10米记为+10米，那么向西走10米记为（）

A . +10米 B . -10米 C . 0米 D . +20米

答案解析收藏纠错 + 选题
2. (2024七上·高州期末) 最适合采用全面调查的是（）

A . 调查全国中学生的睡眠情况 B . 调查初一某班同学课外体育锻炼时间 C . 调查某市居民日平均用水量 D . 调查某种品牌电器的使用寿命

答案解析收藏纠错 + 选题
3. (2024七上·高州期末) 2023年6月7日至11日，第十九届中国（深圳）国际文化产业博览交易会在广东深圳举行，本次共展出超过 $\text{[math]}$ 件文化产品．将 $\text{[math]}$ 用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七上·高州期末) 一个正方体的每个面都写有一个汉字，其表面展开图如题4图所示，则在该正方体中，和“知”相对的面上写的汉字是（）

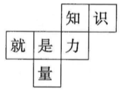
A . 就 B . 是 C . 力 D . 量

答案解析收藏纠错 + 选题
5. (2024七下·海曙期末) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·德惠模拟) 下列日常现象
①用两根钉子就可以把一根木条固定在墙上；②把弯曲的公路改直，就能够缩短路程；③园林工人栽一行树先栽首尾的两棵树；④建筑工人砌墙时，经常先在两端立桩拉线然后沿着线砌墙其中，可以用“两点确定一条直线”来解释的现象是（）

A . ①④ B . ②③ C . ①②④ D . ①③④

答案解析收藏纠错 + 选题
7. (2024七上·高州期末) 一个公园的示意图如题7图所示，在大门北偏东 $\text{[math]}$ 的景点是（）

A . 海洋世界 B . 猴山 C . 虎豹园 D . 大象馆

答案解析收藏纠错 + 选题
8. (2024七上·高州期末) 用符号语言表述“正数的绝对值等于它本身”，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024七上·高州期末) 上午 $\text{[math]}$ 时，钟表的分针与时针夹角的度数是（）

A . 105度 B . 85度 C . 95度 D . 115度

答案解析收藏纠错 + 选题
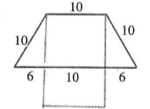
10. (2024七上·高州期末) 墙上钉着用一根彩绳围成的梯形状的饰物，如图实线所示(单位：cm).小颖将梯形下底的钉子去掉，并将这条彩绳钉成一个长方形，如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm，根据题意，可得方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(5个题,每题3分,共15分)

11. (2024七上·高州期末) 在 $\text{[math]}$ 中，底数是，指数是，幂是．

答案解析收藏纠错 + 选题
12. (2024七上·高州期末) 明明步行上学，速度为 $\text{[math]}$ ；亮亮骑自行车上学，速度是明明的2倍，则亮亮的速度可以表示为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024七上·高州期末) 从五边形的一个顶点出发能画出条对角线.

答案解析收藏纠错 + 选题
14. (2024七上·高州期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
15. (2024七上·高州期末) 如图是棋子摆成的“广”字，若按这样的规律摆下去，摆成第10个“广”字需要棋子的枚数是．

答案解析收藏纠错 + 选题

三、解答题(一):本大题共4小题,每小题6分,共24分.

16. (2024七上·高州期末)
1. （1）计算： $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024七上·高州期末) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024七上·高州期末) 一件商品先按成本价提高 $\text{[math]}$ 后标价，再以8折销售，售价为180元．
1. （1）这件商品的成本价是多少？
2. （2）求此件商品的利润率．
答案解析收藏纠错 + 选题
19. (2024七上·高州期末) 把两个三角尺按如图所示那样拼在一起（三角尺分别含 $\text{[math]}$ 角，点A、C、D在一条直线上）
1. （1）求 $\text{[math]}$ 的度数；
2. （2）若 $\text{[math]}$ 是 $\text{[math]}$ 的平分线，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题

四、解答题(二):本大题共3小题,每小题9分,共27分.

20. (2024七上·高州期末) 一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5千米到达小颖家，然后向西走了10千米到达小明家，最后回到超市.
1. （1）以超市为原点，以向东的方向为正方向，用1个单位长度表示1千米，用A，B，C分别表示小明家，小彬家，小颖家，在如图数轴上表示出A，B，C的位置.
2. （2）小明家距小彬家千米.
3. （3）货车一共行驶了多少其纳米？
答案解析收藏纠错 + 选题

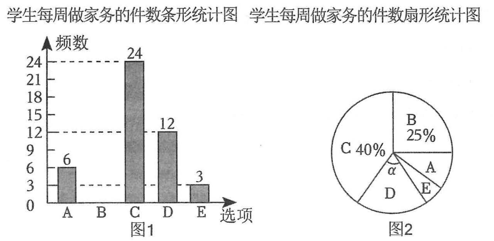
21. (2024七上·高州期末) 教育部印发的《义务教育课程方案》和《课程标准》（2022年版）将劳动从原来的综合活动课中独立出来.某中学为了解学生做家务的情况，随机抽取了若干学生进行了问卷调查，并将数据整理后，绘制成如下不完整的统计图：

调查问卷

在下列家务劳动中①整理房间，打扫卫生；②吃过饭后收拾餐桌，洗刷餐具；③清洗自己的衣服，整理衣柜；④给家里的花草浇水施肥或给小动物喂食洗澡。你每周能主动参与做 ▲件事情.A.零B.一C.二D.三E.四

根据图中信息，请完成下列问题

（1）本次抽样调查的总人数有人；并补全条形统计图.
（2）在扇形统计图中，若选项D所对应的圆心角为 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ；
（3）若规定“每周能主动做三件家务劳动及以上者”为“优秀家务小能手”，已知该校共有学生1800人，请你估计该校能评为“优秀家务小能手”的学生有多少人?

答案解析收藏纠错 + 选题

22. (2024七上·高州期末) 再读教材
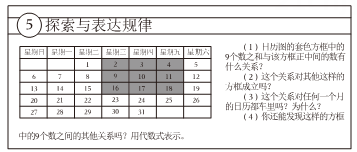
请解答教材中的(1)、(2)问。
活学活用
小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数 $\text{[math]}$ ，排成如图形式，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：
1. （1）十字框中的五个数的和与中间的数16有什么关系?
2. （2）设中间的数为 $\text{[math]}$ ，用代数式表示十字框中的五个数的和；
3. （3）若将十字框上下左右移动，可框住另外的五个数，其它五个数的和能等于2010吗?如能，写出这五个数，如不能，说明理由.
答案解析收藏纠错 + 选题

五、解答题(三):本大题共2小题,共24分.

23. (2024七上·高州期末) 综合与实践：
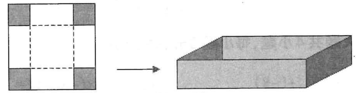
主题：制作一个无盖长方形盒子.
步骤1：按照如图所示的方式，将正方形纸片的四个角剪掉四个大小相同的小正方形.
步骤2：沿虚线折起来，就可以做成一个无盖的长方体盒子.
1. （1）【问题分析】
  如果原正方形纸片的边长为 $\text{[math]}$ ，剪去的正方形的边长为 $\text{[math]}$ ，则折成的无盖长方体盒子的高、底面积、容积分别为、、(请你用含a，b的代数式来表示).
2. （2）如果a=20cm，剪去的小正方形的边长按整数值依次变化，即分别取 $\text{[math]}$ ， $\text{[math]}$ 时，折成的无盖长方体的容积分别是下表数据，请求出 $\text{[math]}$ 和 $\text{[math]}$ 分别是多少?
  剪去正方形的边长 $\text{[math]}$
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  容积 $\text{[math]}$
  324
  512
  m
  n
  500
  384
  252
  128
  36
  0
3. （3）【实践分析】
  观察绘制的统计表，你发现，随着减去的小正方形的边长的增大，所折无盖长方体盒子的容积如何变化?并分析猜想当剪去图形的边长为多少时，所得的无盖长方体的容积最大，此时最大容积是多少?
答案解析收藏纠错 + 选题
24. (2024七上·高州期末) 【材料阅读】
已知 $\text{[math]}$ 是关于 $\text{[math]}$ 的二次二项式，A，B是如图1数轴上两点，且A，B对应的数分别为a，b.C是线段AB的中点.
1. （1） A点对应的数 $\text{[math]}$ ， $\text{[math]}$ 点对应的数 $\text{[math]}$ ，点 $\text{[math]}$ 表示的数是；
2. （2）若点P、Q分别从点C、B同时出发，以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动，则 $\text{[math]}$ 秒后，点P、Q表示的数分别是、（用含t的代数式表示）；
3. （3）在（2）的条件下，若P、Q两点之间的距离为2，求 $\text{[math]}$ 的值.
  【方法迁移】
  如图2， $\text{[math]}$ 平分 $\text{[math]}$ .现有射线OP、OQ分别从OC、OB同时出发，以每秒 $\text{[math]}$ 和每秒 $\text{[math]}$ 的速度绕点 $\text{[math]}$ 顺时针旋转，当OP旋转一周时，这两条射线都停止旋转.问经过几秒后，射线OP、OQ的夹角为 $\text{[math]}$
  【生活运用】
  周末的下午，小明看到钟面显示3点整，此时分针与时针的夹角恰好为 $\text{[math]}$ ，经过多少分钟后，分针与时针的夹角首次变成 $\text{[math]}$
答案解析收藏纠错 + 选题