浙江省杭州市文理中学2023-2024学年七年级上学期数学1...

更新时间：2024-04-25 浏览次数：45 类型：月考试卷

一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．

1. (2024七上·杭州月考) ﹣2024的相反数是（）

A . $\text{[math]}$ B . -2024 C . $\text{[math]}$ D . 2024

答案解析收藏纠错 + 选题
2. (2024七上·杭州月考) 红树林、海草床和滨海盐沼组成三大滨海“蓝碳”生态系统．相关数据显示，按全球平均值估算，我国三大滨海“蓝碳”生态系统的年碳汇量最高可达约3080000吨二氧化碳．将3080000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七上·杭州月考) 下列实数中，为无理数的是（）

A . $\text{[math]}$ B . 1.2012001 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七上·九江期中) 下列两个数互为相反数的是（）

A . 3和 $\text{[math]}$ B . $\text{[math]}$ 和 $\text{[math]}$ C . $\text{[math]}$ 和 $\text{[math]}$ D . $\text{[math]}$ 和 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023七上·余江期中) 下列计算中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七上·杭州月考) 如图所示，从点A到点G，下列路径最短的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七上·杭州月考) 某小组计划做一批中国结，如果每人做6个，那么比计划多做了9个，如果每人做4个，那么比计划少7个．设计划做x个“中国结”，可列方程（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七上·杭州月考) 下列说法中，正确的是（）

A . 如果两个角是同一个角的补角，那么它们相等 B . 如果AC＝BC，那么C是线段AB的中点 C . 如果两个角互补，那么它们的角平分线所在直线的夹角为90° D . 射线AB和射线BA是同一条射线

答案解析收藏纠错 + 选题
9. (2024七上·杭州月考) 如图，数轴上点A、B、C、D所表示的数分别是a、b、c、d，若abcd＜0，ab＞cd，则原点的位置在（）

A . 点A的左边 B . 线段AB上 C . 线段BC上 D . 线段CD上

答案解析收藏纠错 + 选题
10. (2024七上·杭州月考) 如图，把一个周长为定值的长方形分割为五个四边形，其中 $\text{[math]}$ 是正方形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都是长方形，这五个四边形的周长分别用 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 表示，则下列各式的值为定值的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本题有6个小题，每小题4分，共24分．

11. (2024七上·杭州月考) 单项式-2ab²的系数是，次数是.

答案解析收藏纠错 + 选题
12. (2024九下·南宁模拟) 若 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，则m＝．

答案解析收藏纠错 + 选题
13. (2024七上·杭州月考) $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2024七上·杭州月考) 已知∠1＝53°29^' ，则∠1的余角是．（填具体角度）

答案解析收藏纠错 + 选题
15. (2024七上·杭州月考) 已知关于x的一元一次方程 $\text{[math]}$ 的解为x＝2，那么关于y的一元一次方程 $\text{[math]}$ 的解为y＝．

答案解析收藏纠错 + 选题
16. (2024七上·杭州月考) 观察下列两列数：
－2，－4，－6，－8，－10，－12，…
－2，－5，－8，－11，－14，－17，…
通过探究可以发现，第1个相同的数是－2，第2相同的数是－8，…．则第4个相同的数
是．若第n个相同的数是－2024，则n＝．

答案解析收藏纠错 + 选题

三、解答题：本大题有8个小题，共66分．解答应写出文字说明、证明过程或演算步骤.

17. (2024七上·杭州月考) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024七上·杭州月考) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2024七下·合肥期中) 老师在黑板上写了一个正确的演算过程，随后用手掌捂住了多项式形式如下：
$\text{[math]}$
1. （1）求所捂的多项式；
2. （2）若a，b满足： $\text{[math]}$ ，请求出所捂的多项式的值．
答案解析收藏纠错 + 选题
20. (2024七上·杭州月考) 如图，已知线段AB＝23，BC＝15，点M是AC的中点．
1. （1）求线段AM的长；
2. （2）在线段CB上取一点N，使得CN：NB＝1：2，求线段MN的长．
答案解析收藏纠错 + 选题

21. (2024七上·杭州月考) 用A，B两种型号的机器生产相同的产品，产品装入同样规格的包装箱后运往仓库．已知每台B型机器比A型机器一天多生产2件产品，3台A型机器一天生产的产品恰好能装满5箱，4台B型机器一天生产的产品恰好能装满7箱．每台A型机器一天生产多少件产品？每箱装多少件产品？

下面是解决该问题的两种方法，请选择其中的一种方法，完成分析填空和解答．

【方法一】分析：设每箱装x件产品，则3台A型机器一天共生产① ▲ )件产品，4台B型机器一天共生产( ▲ )件产品，再根据题意列方程．

解：设每箱装x件产品．

答：（写出完整的解答过程）

【方法二】分析：设每台A型机器一天生产x件产品，则每台B型机器一天生产（x+2）件产品，3台A型机器一天共生产(① ▲ )件产品，4台B型机器一天共生产(② ▲ )件产品，再根据题意列方程．

解：设每台A型机器一天生产x件产品

答：（写出完整的解答过程）

答案解析收藏纠错 + 选题

22. (2024七上·杭州月考) 某超市将每个进价为10元的文具袋以每个16元的销售价售出，平均每月能售出250个．市场调研表明：当每个文具袋的销售价下降1元时，其月销售量增加60个．若设每个文具袋的销售价下降m元．
1. （1）试用含m的式子填空：
  ①降价后，每个文具袋的利润为()元（利润＝销售价－进价）；
  ②降价后，该超市的文具袋平均每月销售量为()个；
2. （2）如果（1）中的m＝4，请计算该超市该月销售这种文具袋的利润是多少元（总利润＝单个利润×销售数量）？
答案解析收藏纠错 + 选题
23. (2024七上·庐江期末) 已知∠AOB＝75°，射线OC在∠AOB的内部，且∠AOC＝4∠BOC．射线OD是平面上绕点O旋转的一条动射线，OE平分∠DOC．
1. （1）如图1，射线OD在∠AOC的内部．
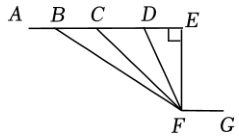
  ①求∠BOC的度数；
  ②若∠EOC与∠DOB互余，求∠EOC的度数；
2. （2）若∠AOD＝n°（0＜n＜60），直接写出∠BOE的度数（用含n的式子表示）．
答案解析收藏纠错 + 选题
24. (2024七上·杭州月考) 在数轴上，点O表示的数为0，点M表示的数为m（m≠0）．给出如下定义：对于该数轴上的一点P与线段OM上一点Q，如果线段PQ的长度有最大值，那么称这个最大值为点P与线段OM的“闭距离”．如图1，若m＝－1，点P表示的数为3，当点Q与点M重合时，线段PQ的长最大，值是4，则点P与线段OM的“闭距离”为4．
1. （1）如图2，在该数轴上，点A表示的数为－1，点B表示的数为2．
  ①当m＝1时，点A与线段OM的“闭距离”为；
  ②若点B与线段OM的“闭距离”为3，求m的值；
2. （2）在该数轴上，点C表示的数为－m，点D表示的数为－m＋3，若线段CD上存在点G，使得点G与线段OM的“闭距离”为5，直接写出m的最大值与最小值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省杭州市文理中学2023-2024学年七年级上学期数学1...

副标题：

*注意事项：

浙江省杭州市文理中学2023-2024学年七年级上学期数学1...

试题分析

总体分析

题量分析

难度分析

知识点分析