湖南省岳阳市岳阳县2023-2024学年九年级上学期数学期末...

更新时间：2024-04-17 浏览次数：19 类型：期末考试

一、选择题(本大题共 10小题，每小题 3 分，满分 30 分．在每小题给出的四个选项中，选出符合要求的一项)

1. (2024九上·岳阳期末) 在下列方程中，是一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·岳阳期末) 在 Rt△ABC中，∠C= 90°，若 △ABC的三边都放大2倍，则 sinA的值（）

A . 缩小 2 倍 B . 放大 2 倍 C . 不变 D . 无法确定

答案解析收藏纠错 + 选题
3. (2024九上·岳阳期末) 甲、乙、丙、丁四名学生参加市中小学生运动会跳高项目预选赛，他们 8次跳高的平均成绩都相同，他们的方差按顺序分别是 0.32 、0.52 、0.46 、0.23，现在要选一名成绩较好且稳定的运动员去参赛，应选运动员（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
4. (2024九上·岳阳期末) 某反比例函数图象上四个点的坐标分别为 $\text{[math]}$ ，则， $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·岳阳期末) 把方程 x²+6x -5 = 0化成 (x+m)²=n的形式，则 m+n的值为（）

A . 17 B . 14 C . 11 D . 7

答案解析收藏纠错 + 选题
6. (2024九上·岳阳期末) 把二次函数y＝（x-3）²+6的图像向左平移1个单位，再向下平移2个单位后得到的二次函数为（）

A . y＝（x-4）²+4 B . y＝（x-2）²+4 C . y＝（x-2）²+8 D . y＝（x-4）²+8

答案解析收藏纠错 + 选题
7. (2024九上·岳阳期末) 如图， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
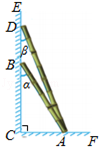
8. (2024九上·岳阳期末) 如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α，∠ADC=β，则竹竿AB与AD的长度之比为（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. 若关于x的一元二次方程 $\text{[math]}$ 两根为 $\text{[math]}$ ，且 $\text{[math]}$ ，则m的值为（）

A . 4 B . 8 C . 12 D . 16

答案解析收藏纠错 + 选题
10. (2024九上·岳阳期末) 如图，Rt△AOB的直角顶点O与坐标原点重合，∠OAB=30°，若A点在反比例函数 $\text{[math]}$ 的图象上，则过B点的反比例函数的比例系数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . 2

答案解析收藏纠错 + 选题

二、填空题(本大题共 6 小题，每小题 3分，满分18 分)

11. (2024九上·岳阳期末) 已知反比例函数 $\text{[math]}$ ，当x＞0时，函数y随x的增大而；

答案解析收藏纠错 + 选题
12. (2024九上·岳阳期末) 在直角三角形ABC中，若∠C=90°，AC=3，BC=4，则tanA=；

答案解析收藏纠错 + 选题
13. (2024九上·岳阳期末) 某滑雪运动员沿坡比为1∶ $\text{[math]}$ 的斜坡滑下30米，那么他下降的高度为米.

答案解析收藏纠错 + 选题
14. (2024九上·岳阳期末) 关于x的方程 $\text{[math]}$ 有两个相等的实数根，其中∠A是锐角三角形ABC的一个内角，则∠A=。

答案解析收藏纠错 + 选题
15. (2024九上·岳阳期末) 二次函数y＝x²-2x+m与x轴的一个交点为（-1，0），则关于x的一元二次方程x²-2x+m=0的解为；

答案解析收藏纠错 + 选题
16. (2024九上·岳阳期末) 已知a、b是方程 $\text{[math]}$ 的两根，则代数式 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题(本大题共9题，满分72 分，解答应写出文字说明，证明过程或演算步骤)

17. (2024九上·岳阳期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2024九上·岳阳期末) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2024九上·岳阳期末) 在 $\text{[math]}$ 中， $\text{[math]}$ 是斜边 $\text{[math]}$ 上的高．
1. （1）证明： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2024九上·岳阳期末) 第七届全国学生“学宪法、讲宪法 ”活动开展以来，全国各地师生积极响应。某校为了解本校学生对宪法知识的情况，对八年级学生进行了知识测试，测试成绩全部合格，现随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：
分数段
频数
频率
60 ≤ x＜70
9
a
70 ≤ x＜80
36
0.4
80 ≤ x＜90
27
0.3
90 ≤ x＜100
b
0.2
请根据上述统计图表，解答下列问题：
1. （1）表中 a= ， b= ；
2. （2）请补全频数分布直方图；
3. （3）根据以上数据，如果 90分以上(含 90分)为优秀，若该学校八年级学生有 900名，请你估算一下该学校八年级学生成绩优秀的人数.
答案解析收藏纠错 + 选题
21. (2024九上·岳阳期末) 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 为常数且 $\text{[math]}$ 的图象相交于 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求反比例函数的表达式；
2. （2）将一次函数 $\text{[math]}$ 的图象沿 $\text{[math]}$ 轴向下平移b个单位 $\text{[math]}$ ，使平移后的图象与反比例函数的 $\text{[math]}$ 图象有且只有一个交点，求b的值．
答案解析收藏纠错 + 选题
22. (2024九上·岳阳期末) nbsp；．随着科技的发展，无人机已广泛应用于生产生活，如代替人们在高空测量距离和高度．小明要测量教学楼 $\text{[math]}$ 的高度，借助无人机设计了如下测量方案：如图，小明在离教学楼底部 $\text{[math]}$ 米的C处，遥控无人机旋停在点C的正上方的点D处，测得教学楼 $\text{[math]}$ 的顶部B处的俯角为 $\text{[math]}$ ， $\text{[math]}$ 长为 $\text{[math]}$ 米．已知目高 $\text{[math]}$ 为 $\text{[math]}$ 米．
1. （1）求教学楼 $\text{[math]}$ 的高度．
2. （2）若无人机保持现有高度沿平行于 $\text{[math]}$ 的方向，以 $\text{[math]}$ 米/秒的速度继续向前匀速飞行，求经过多少秒时，无人机刚好离开小明的视线 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2024九上·岳阳期末) 公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔4月份到6月份的销量，该品牌头盔4月份销售150个，6月份销售216个，且从4月份到6月份销售量的月增长率相同．
1. （1）为求该品牌头盔销售量的月增长率，设增长率为a ，依题意列方程为；
2. （2）若此种头盔的进价为30元 $\text{[math]}$ 个，测算在市场中，当售价为40元 $\text{[math]}$ 个时，月销售量为600个，若在此基础上售价每涨价1元 $\text{[math]}$ 个，则月销售量将减少10个，若该品牌头盔涨价x元 $\text{[math]}$ 个，销售总利润为y ，列出y与x的函数关系式.
  ①当x为多少时？销售总利润达到10000元.
  ②当x为多少时？销售总利润达到最大，求最大总利润.
答案解析收藏纠错 + 选题
24. (2024九上·岳阳期末) 某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：
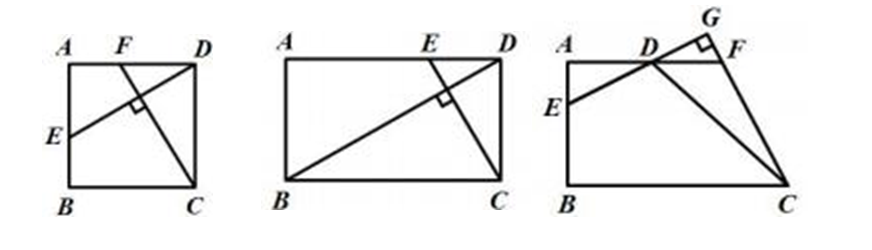
1. （1）【观察与猜想】如图 1 ，在正方形 ABCD中，点 E、 F分别是 AB、AD上的两点，连接DE、 CF ， DE⊥CF ，则 $\text{[math]}$ 的值为；
2. （2）【类比探究】如图 2 ，在矩形ABCD中， ∠DBC=30° ，点E是AD上的一点，连接CE、BD，且CE⊥BD ，求 $\text{[math]}$ 的值；
3. （3）【拓展延伸】如图 3 ，在四边形ABCD中，∠A=∠B=90°，AB=m ， AD=n ，点E为AB上一点，连接DE ，过点C作DE的垂线交ED的延长线于点G ，交AD的延长线于点F ，求 $\text{[math]}$ 的值；
答案解析收藏纠错 + 选题
25. (2024九上·岳阳期末) 我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于y轴对称，则把该函数称之为“T函数”，其图象上关于y轴对称的不同两点叫做一对“T点”．根据该约定，完成下列各题．
1. （1）若关于x的函数y＝(m+1)x²+(m²-1)x是“T函数”，求m的值；
2. （2）若点A（1，r）与点B（s ， 4）是关于x的“T函数”y＝ $\text{[math]}$ 的图象上的一对“T点”，求r ， s ， t的值；
3. （3）若关于x的“T函数”y＝ax²+bx+c（a＞0，且a ， b ， c是常数）经过坐标原点O ，且与直线l：y＝mx+n（m≠0，n＞0，且m ， n是常数）交于M（x₁ ， y₁），N（x₂ ， y₂）两点，当x₁ ， x₂满足x₁+x₂＝x₁x₂时，直线l是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由．
答案解析收藏纠错 + 选题