一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
-
-
4.
(2024八上·成都期末)
如图,这是一个利用平面直角坐标系画出的某学校的示意图,如果这个坐标系以正东方向为

轴的正方向,以正北方向为

轴的正方向,并且综合楼和教学楼的坐标分别是

和

, 则食堂的坐标是( )
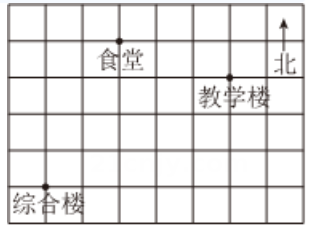
-
5.
(2024八上·成都期末)
甲、乙、丙、丁四名同学参加立定跳远训练,他们成绩的平均数相同,方差如下:

,

,

,

, 则成绩最稳定的是( )
A . 甲
B . 乙
C . 丙
D . 丁
-
A .  B .
B .  C . 5
D . 10
C . 5
D . 10
-
7.
(2024八上·成都期末)
某城市几条道路的位置关系如图所示,道路

, 道路

与

的夹角

, 城市规划部门想新修一条道路

, 要求

, 则

的度数为( )
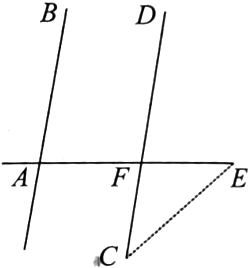
-
A . 函数值 随自变量
随自变量 的增大而减小
B . 图象与
的增大而减小
B . 图象与 轴交于点
轴交于点 C . 点
C . 点 在函数图象上
D . 图象经过第二、三、四象限
在函数图象上
D . 图象经过第二、三、四象限
二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
-
11.
(2024八上·成都期末)
下表是小明参加一次“青春风采”才艺展示活动比赛的得分情况:
总评分时,按书法占40%,舞蹈占30%,演唱占30%考评,则小明的最终得分为.
-
-
13.
(2024八下·中山期中)
如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢

飞到另一棵树的树梢

, 则小鸟至少要飞行
米.

三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
-
-
(1)
计算:

;
-
(2)
解方程组:

.
-
15.
(2024八上·成都期末)
学校组织七、八年级学生参加体育综合素质评价测试,已知七、八年级各有160人,现从两个年级分别随机抽取8名学生的测试成绩(单位:分)进行统计.
七年级:89,87,91,91,93,98,94,97
八年级:98,84,92,93,95,95,88,95
整理如下:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 92.5 | 
| 91 |
八年级 | 92.5 | 94 | 
|
根据以上信息,回答下列问题:
-
(1)
填空:

,

;
-
(2)
甲同学说:“这次测试我得了93分,位于年级中等偏上水平”,你认为甲同学在哪个年级,并简要说明理由;
-
(3)
若规定测试成绩不低于90分为“优秀”,估计该学校这两个年级测试成绩达到“优秀”的学生总人数.
-
-
-
(2)
已知点

的坐标为

, 判断

的形状,并说明理由.
-
17.
(2024八上·成都期末)
某单位准备购买一种水果,现有甲、乙两家超市进行促销活动,该水果在两家超市的标价均为13元/千克.甲超市购买该水果的费用

(元)与该水果的质量

(千克)之间的关系如图所示;乙超市该水果在标价的基础上每千克直降3元.
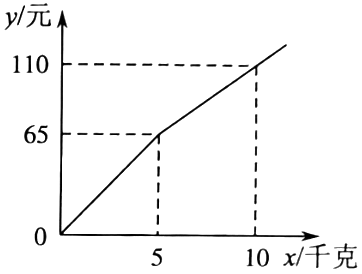
-
(1)
求

与

之间的函数表达式;
-
(2)
现计划用290元购买该水果,选甲、乙哪家超市能购买该水果更多一些?
-
-
-
(2)
如图2,当点

在

外部,连接

, 若

,

, 求线段

的长;
-
(3)
如图3,当点

在

内部,连接

, 若

,

, 求点

到

的距离.
四、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
-
21.
(2024八上·成都期末)
如图,在平面直角坐标系

中,

的顶点坐标分别为

,

,

, 点

在

轴右侧,若以

,

,

为顶点的三角形与

全等,则点

的坐标为
.

-
-
23.
(2024八上·成都期末)
定义:若三个正整数

,

,

满足

,

, 且

, 则称

为“偶差”勾股数组.例如:

,

都是“偶差”勾股数组.令

, 将

从小到大排列,分别记为

,

,

, …,

(

为正整数),则

的值为
.
五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24.
(2024八上·成都期末)
2023年12月4日至10日,国际乒联混合团体世界杯在四川成都举行,在此期间,成都某酒店对三人间及双人间客房进行优惠大酬宾,优惠方案为:三人间为每天每间360元,双人间为每天每间300元,一个40人的旅游团于2023年12月4日在该酒店人住,住了一些三人间及双人间客房,且每个客房正好住满.
-
(1)
若旅游团一天共花去住宿费5100元,求该旅行团租住了三人间、双人间各多少间?
-
(2)
设有

人住三人间,这个团一天共花去住宿费

元,请求出

与

的函数表达式.
-
25.
(2024八上·成都期末)
如图1,在边长为2的正方形

中,点

是射线

上一动点,连接

, 以

为边在直线

右侧作正方形

.
图1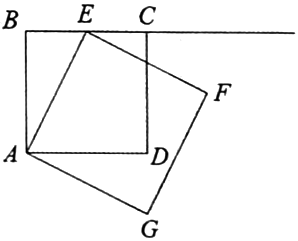 图2
图2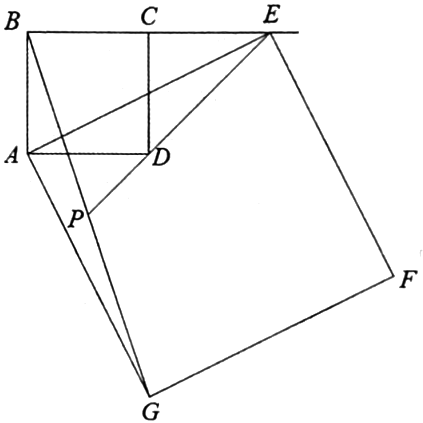
-
-
-
(3)
如图2,点

在线段

的延长线上,连接

, 若

的延长线恰好经过

的中点

, 求线段

的长.
-
-
(1)
求

的面积;
-
(2)
若点

的横坐标为1,直线

上是否存在点

, 使点

到直线

的距离为

, 若存在,求出点

的坐标,若不存在,请说明理由;
-
(3)
将

沿直线

翻折,点

的对应点为

, 若

为直角三角形,求线段

的长.

