浙江省湖州市长兴县龙山共同体2023-2024学年八年级下学...

更新时间：2024-04-12 浏览次数：30 类型：月考试卷

一、单选题(本大题有10小题,每小题3分,共30分)

1. (2024八下·长兴月考) 若代数式 $\text{[math]}$ 有意义，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·长兴月考) 方程 $\text{[math]}$ 的根是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·重庆市期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·湖北期中) 下列各式中，属于最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·佳木斯月考) 用配方法解方程 $\text{[math]}$ 时，配方结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·开州模拟) 一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
7. (2024八下·荣成期中) 若 $\text{[math]}$ 是关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ 的值是（）

A . 2024 B . 2023 C . 2022 D . 2021

答案解析收藏纠错 + 选题
8. (2024八下·长兴月考) 已知实数x，y满足 $\text{[math]}$ ，则以x，y的值为两边长的等腰三角形的周长是（）

A . 10 B . 14 C . 16 D . 16或14

答案解析收藏纠错 + 选题
9. (2024八下·长兴月考) 已知m、n是两个连续自然数（m＜n），且 $\text{[math]}$ ， $\text{[math]}$ ，则p（）

A . 总是奇数 B . 总是偶数 C . 有时奇数，有时偶数 D . 有时是有理数，有时是无理数

答案解析收藏纠错 + 选题
10. (2024八下·长兴月考) 关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ ，下列说法中：
①若 $\text{[math]}$ ，则 $\text{[math]}$ ；
②若方程 $\text{[math]}$ 有两个不相等的实根，则方程 $\text{[math]}$ 必有两个不相等的实根；
③若 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根，则一定有 $\text{[math]}$ 成立；
④若 $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的根，则 $\text{[math]}$
其中正确的：（）

A . 只有① B . 只有①② C . 只有①②③ D . 只有①②④

答案解析收藏纠错 + 选题

二、填空题(本大题有6小题,每小题4分,共24分)

11. (2024八下·长兴月考) 化简 $\text{[math]}$ 的结果是.

答案解析收藏纠错 + 选题
12. (2024八下·长兴月考) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的一个根是3，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
13. (2024八下·长兴月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2024八下·长兴月考) 实数a，b在数轴上的位置如图所示，则化简 $\text{[math]}$ 的结果是.

答案解析收藏纠错 + 选题
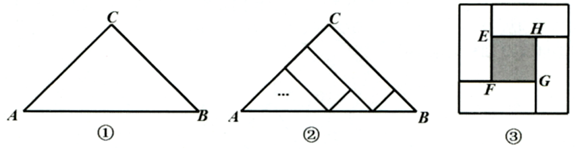
15. (2024八下·长兴月考) 如图①是一张等腰直角三角形纸片， $\text{[math]}$ ，现要求按照图②的方法裁剪几条宽度都为 $\text{[math]}$ 的长方形纸条，用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③，正方形美术作品的面积为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2024八下·长兴月考) 新定义：关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 与 $\text{[math]}$ 称为“同族二次方程”.例如： $\text{[math]}$ 与 $\text{[math]}$ 是“同族二次方程”.现有关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 与 $\text{[math]}$ 是“同族二次方程”，则代数式 $\text{[math]}$ 的最小值是.

答案解析收藏纠错 + 选题

三、解答题(本大题有8小题,共66分)

17. (2024八下·长兴月考) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2024八下·余姚期中) 解下列方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2024八下·长兴月考) 已知 $\text{[math]}$ ，求下列式子的值：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
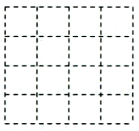
20. (2024八下·长兴月考) 如图，在 $\text{[math]}$ 的正方形网格中，每个小格的顶点叫做格点，设顶点在格点上的三角形为格点三角形，按下列要求画图.
1. （1）请你在网格图中画出边长为 $\text{[math]}$ 的格点三角形；
2. （2）在(1)的条件下，求三角形最长边上的高.
答案解析收藏纠错 + 选题
21. (2024八下·长兴月考) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$
1. （1）求证：无论 $\text{[math]}$ 取何值，方程总有实数根；
2. （2）若等腰三角形ABC的底边长为5，另两边的长恰好是这个方程的两个根，求 $\text{[math]}$ 的周长
答案解析收藏纠错 + 选题

22. (2024八下·长兴月考) 根据以下销售情况，解决销售任务.

	销售情况分析
	总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，它们的销售情况如下：
店面	甲店	乙店
日销售情况	每天可售出20件，每件盈利40元.	每天可售出32件，每件盈利30元.
市场调查	经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件.
情况设置	设甲店每件衬衫降价 $\text{[math]}$ 元，乙店每件衬衫降价 $\text{[math]}$ 元.
任务解决
任务（1）	甲店每天的销售量 ▲ (用含 $\text{[math]}$ 的代数式表示). 乙店每天的销售量 ▲ (用含 $\text{[math]}$ 的代数式表示).
任务（2）	当 $\text{[math]}$ 时，分别求出甲、乙店每天的盈利.
任务（3）	总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和为2244元.

答案解析收藏纠错 + 选题

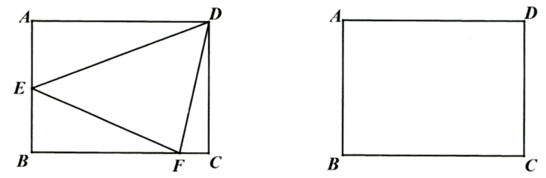
23. (2024八下·长兴月考) 如图，在长方形ABCD中， $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以 $\text{[math]}$ 的速度沿 $\text{[math]}$ 的方向向点 $\text{[math]}$ 运动，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，以 $\text{[math]}$ 的速度向点 $\text{[math]}$ 运动.若 $\text{[math]}$ 、 $\text{[math]}$ 两点同时出发，其中一点运动到终点另一点也停止运动，设运动时间为ts，连结DE、DF.
1. （1）当t=1时，四边形DEBF的面积等于 $\text{[math]}$ .
2. （2）当 $\text{[math]}$ 为何值时，线段EF长为 $\text{[math]}$ ?
3. （3）当 $\text{[math]}$ 为何值时， $\text{[math]}$ 的面积为 $\text{[math]}$ ?
答案解析收藏纠错 + 选题
24. (2024八下·长兴月考) 阅读材料：
已知a，b为非负实数， $\text{[math]}$
$\text{[math]}$ ，当且仅当“ $\text{[math]}$ ”时，等号成立.
这个结论就是著名的“均值不等式”，“均值不等式”在一类最值问题中有着广泛的应用.
例：已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 最小值.
解：令 $\text{[math]}$ ，则由 $\text{[math]}$ ，得 $\text{[math]}$ .
当且仅当 $\text{[math]}$ ，即 $\text{[math]}$ 时，代数式取到最小值，最小值为6.
根据以上材料解答下列问题：
1. （1）【灵活运用】
  已知 $\text{[math]}$ ，则当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 取到最小值，最小值为.
2. （2）已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的最小值.
3. （3）【拓展运用】
  某校要对操场的一个区域进行改造，利用一面足够长的墙体将该区域用围栏围成中间隔有两道围栏的矩形花圃，如图1所示，为了围成面积为 $\text{[math]}$ 的花圃，所用的围栏至少为多少米?
4. （4）如图2，四边形ABCD的对角线AC，BD相交于点 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别是4和12，求四边形ABCD面积的最小值.
答案解析收藏纠错 + 选题