河北省孟村回族自治县王史中学2023-2024学年九年级下学...

更新时间：2024-06-12 浏览次数：8 类型：开学考试

一、选择题（本大题共16个小题，共38分．1-6小题各3分，7-16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024九下·孟村开学考) 规定：（2）表示上升2个台阶记作+2，则（4）表示下降4个台阶记作（）

A . +4 B . -4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·孟村开学考) 借助圆规可以比较线段 $\text{[math]}$ 与 $\text{[math]}$ 的大小，如图所示，下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定 $\text{[math]}$ 与 $\text{[math]}$ 的大小

答案解析收藏纠错 + 选题
3. (2024九下·孟村开学考) $\text{[math]}$ 是 $\text{[math]}$ 的（）

A . 2倍 B . 4倍 C . 6倍 D . 9倍

答案解析收藏纠错 + 选题
4. (2024九下·孟村开学考) 一块矩形的田地被分割成了四个小矩形播种不同的农作物，它们的边长如图所示，则大矩形的面积表示错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·孟村开学考) 如图，将四根长度分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的木条钉成一个四边形木架，为使其稳定，新增的木条 $\text{[math]}$ 的长度可能是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·孟村开学考) 将两个实数用科学记数法表示为 $\text{[math]}$ ， $\text{[math]}$ 下列正确的是（）

A . M ， N均为正数 B . M ， N均为负数 C . M是正数，N是负数 D . M是负数，N是正数

答案解析收藏纠错 + 选题
7. (2024九下·孟村开学考) 根据图中嘉淇和小宇的对话，可以判断他们共同搭的几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2024九下·孟村开学考) 一个不透明的口袋里有4个黄球和4个红球，除颜色不同外其余均相同，将所有球混合均匀后随机摸出1个球，要使摸出黄球的可能性大于摸出红球的可能性，可以在摸球之前（）

A . 拿出2个黄球 B . 拿出2个红球 C . 放入2个白球 D . 放入2个红球

答案解析收藏纠错 + 选题
9. (2024九下·孟村开学考) 在如图所示的正方形网格中，△ABC的三个顶点A ， B ， C均在格点上，O是AC边的中点，利用△ABC在网格中作平行四边形ABCD ，甲和乙给出了如下方案：
甲：作点B关于点O的对称点D ，连接AD ， CD；
乙：将△ABC绕点O旋转180°得到△EDF ，其中，点A的对应，点B为点E ，点B的对应点为点D ，点C的对应点为点F图5对于甲、乙两个方案，判断正确的是（）

A . 两个方案都可行 B . 两个方案都不可行 C . 甲可行，乙不可行 D . 甲不可行，乙可行

答案解析收藏纠错 + 选题
10. (2024九下·孟村开学考) 如图，直线 $\text{[math]}$ ， △ABC是等边三角形，若∠α=20°，则∠B=（）

A . 130° B . 140° C . 150° D . 160°

答案解析收藏纠错 + 选题
11. (2024九下·孟村开学考) 图是一种正方形ABCD轨道示意图．现有两个机器人P ， Q（看成点）从点A同时出发，沿着轨道以大小相同的速度匀速移动，其路线分别为A→B→C和A→D→C ．若移动时间为x ，两个机器人之间的距离为y ，则y与x关系的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
12. (2024九下·孟村开学考) 如图，以点O为圆心，以任意长为半径画弧①，分别交OA ， OB于点E ， F ，要使∠AOC=∠AOB ，关于弧②的画法及作图依据，下列说法正确的是（）

A . 以点F为圆心，OE长为半径画弧② B . 以点F为圆心，EF长为半径画弧② C . 使∠AOC=∠AOB的依据是SSS D . 使∠AOC=∠AOB的依据是SAS

答案解析收藏纠错 + 选题
13. (2024九下·孟村开学考) 已知水平放置半径为6cm的球形容器中装有溶液，容器内液面的面积为 $\text{[math]}$ ，图是该容器的一个最大纵截面，则该截面⊙O中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2024九下·孟村开学考) 将双曲线 $\text{[math]}$ 与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴之间的区域记为 $\text{[math]}$ （不包括坐标轴与双曲线），若区域 $\text{[math]}$ 内整点（横、纵坐标均为整数）的个数不少于5个，则 $\text{[math]}$ 的值可以是（）

A . 2 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2024九下·孟村开学考) 有一等腰三角形ABC纸片，AB=AC ，沿图中三条虚线将该三角形纸片进行裁剪，相关数据如图所示，裁剪后得到甲、乙、丙、丁四个部分，其中面积最大的是（）

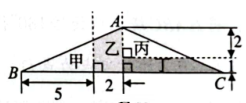
A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
16. (2024九下·孟村开学考) 题目：“已知二次函数 $\text{[math]}$ 的图象 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作直线 $\text{[math]}$ 平行于 $\text{[math]}$ 轴，将抛物线 $\text{[math]}$ 位于直线 $\text{[math]}$ 下方的部分翻折至直线 $\text{[math]}$ 上方，将这部分图象与拋物线 $\text{[math]}$ 剩余部分组成的新图象记为 $\text{[math]}$ ．若图象 $\text{[math]}$ 与 $\text{[math]}$ 轴有4个交点，求 $\text{[math]}$ 的取值范围．”对于其答案，甲答： $\text{[math]}$ ，乙答： $\text{[math]}$ ，丙答： $\text{[math]}$ ，则正确的是（）

A . 只有甲答的对 B . 只有乙答的对 C . 甲、丙答案合在一起才完整 D . 乙、丙答案合在一起才完整

答案解析收藏纠错 + 选题

二、填空题（本大题共3个小题，共10分．17小题2分，1819小题各4分，每空2分）

17. (2024九下·孟村开学考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2024九下·孟村开学考) 已知分式 $\text{[math]}$ 为常数）满足表格中的信息．
根据表中的数据，写出 $\text{[math]}$ 的值为， $\text{[math]}$ 的值为．
$\text{[math]}$
2
0.5
$\text{[math]}$
分式的值
无意义
0
3

答案解析收藏纠错 + 选题
19. (2024九下·孟村开学考) 如图1的螺丝钉由头部（直六棱柱）和螺纹（圆柱）组合而成，其俯视图如图2所示．珍珍想用一把刻度尺测量出螺纹直径，已知刻度尺紧贴螺纹（刻度尺 $\text{[math]}$ 与 $\text{[math]}$ 相切），经过点 $\text{[math]}$ 且交 $\text{[math]}$ 于点 $\text{[math]}$ ．
图1图2
1. （1）正六边形ABCDEF的外角和为°；
2. （2）若测得正六边形ABCDEF的边长为6，AP长为 $\text{[math]}$ ，则螺纹的直径为．
答案解析收藏纠错 + 选题

三、解答题（本大题共7个小题，共72分．解答应写出文字说明、证明过程或演算步骤）

20. (2024九下·孟村开学考) 如图，数轴的单位长度为1，点A ， B ， C ， D所表示的数字分别为a ， b ， c ， d ．
1. （1）当点C为原点时，求a+b+c+d的值；
2. （2）若a+b=-20，求d的值．
答案解析收藏纠错 + 选题
21. (2024九下·孟村开学考) 有甲、乙两块草地，其长和宽的数据如图1所示，其面积分别为 $\text{[math]}$ ， $\text{[math]}$ ．
图1图2
1. （1）请用含m的式子分别表示 $\text{[math]}$ 、 $\text{[math]}$ ；当m=2时，求 $\text{[math]}$ 的值；
2. （2）若再开辟一块正方形草地，记为丙草地，如图2，其面积为 $\text{[math]}$ ，其周长与乙草地的周长相等．
  ①丙草地的边长为（用含m的代数式表示）；
  ②请比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小，并说明理由．
答案解析收藏纠错 + 选题
22. (2024九下·孟村开学考) 某校为了解学生校外的劳动表现，对全校学生进行了问卷调查，让每位学生的家长对自家孩子打分，满分为10分（分数均为整数）．劳动老师从全部的问卷中随机抽取了80份，如下是家长所打分数的频数统计表．
分数（分）
5
6
7
8
9
10
频数
4
8
20
24
16
8
1. （1）求被抽取的家长们所打分数的平均数、中位数和众数；
2. （2）劳动老师从余下的问卷中又随机抽取了1份，与之前的80份合在一起，重新计算后，发现家长所打分数的平均数提高了至少0.15%，求劳动老师最后抽取的问卷中家长所打分数最少为几分？
答案解析收藏纠错 + 选题
23. (2024九下·孟村开学考) 如图1，篮球场上，一名身高为1.85m的运动员跳起投篮，当跳离地面的高度为0.25m时，球在头顶上方0.15m处出手，然后准确落入篮筐，篮球（看成点）的运动路径为抛物线L的一部分．建立如图所示的平面直角坐标系，已知篮筐中心到地面的距离为3.05m，当球与篮筐中心的水平距离为1.5m时，球达到最大高度3.5m．
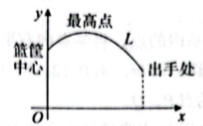
图1图2
1. （1）求：①运动员投球的出手高度；
  ②抛物线L的解析式；
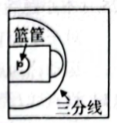
2. （2）图2为篮球场平面示意图，在三分线外投篮得3分，在三分线内投篮得2分．已知三分线与篮筐中心的水平距离为6.75m，请通过计算判断运动员此次投篮的得分．
答案解析收藏纠错 + 选题
24. (2024九下·孟村开学考) 如图，⊙O的半径为2，点A ， B ， C ， D ， E ， F是⊙O的六等分点．过点D作⊙O的切线DG交AE的延长线于点G ．
1. （1）连接DE ，判断DE与AG的位置关系，并说明理由；
2. （2）求线段DG与 $\text{[math]}$ 的长度，并比较大小；
3. （3）若点P是⊙O上任意一点，连接PG ，直接写出PG长的最小值．
答案解析收藏纠错 + 选题
25. (2024九下·孟村开学考) 对于平面直角坐标系内的点，将某点向右平移1个单位长度，再向上平移2个单位长度的运动称为点的斜平移．例如：点P（2，3）经过1次斜平移后得到，点Q（3，5）．
1. （1）设直线l经过上述的点P ， Q ，
  ①求l的解析式并在图中直接画出直线l的图象；
  ②若点P经过m次斜平移后得到点的坐标为（x ， y），用含m的式子分别表示x ， y ，并分析点（x ， y）是否在直线l上；
2. （2）已知点A（-4，-4），点A经过n次斜平移后得到点B ，点B关于直线l的对称点为点C（4，2），直接写出n的值．
答案解析收藏纠错 + 选题
26. (2024九下·孟村开学考) 如图1和2，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿折线 $\text{[math]}$ 运动，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到 $\text{[math]}$ ，旋转角等于 $\text{[math]}$ ，连接 $\text{[math]}$ ．设点 $\text{[math]}$ 在折线 $\text{[math]}$ 上运动的路径长为 $\text{[math]}$ ．
图1图2
1. （1）当点 $\text{[math]}$ 在 $\text{[math]}$ 上时，
  ①作 $\text{[math]}$ 于 $\text{[math]}$ ，如图17-1，求证： $\text{[math]}$ ；
  ②当点 $\text{[math]}$ 恰巧落在边 $\text{[math]}$ 上时，如图17-2，求 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
3. （3）连接 $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 运动到点 $\text{[math]}$ 的过程中，直接写出 $\text{[math]}$ 长的最小值．
答案解析收藏纠错 + 选题