广东省深圳市南山实验教育集团麒麟中学2023-2024学年九...

更新时间：2024-05-09 浏览次数：30 类型：开学考试

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. (2024九下·南山开学考) 如图所示的是某用户微信支付情况，-100表示的意思是（）

A . 发出100元红包 B . 收入100元 C . 余额100元 D . 抢到100元红包

答案解析收藏纠错 + 选题
2. (2024九下·南山开学考) 九 $\text{[math]}$ 班选派 $\text{[math]}$ 名学生参加演讲比赛，他们的成绩如下：
选手
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
平均成绩
中位数
成绩 $\text{[math]}$ 分
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
则如表中被遮盖的两个数据从左到右依次是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·南山开学考) 如图是一个正方体的平面展开图，若正方体中相对的面上的数字或代数式的乘积都小于 $\text{[math]}$ ，则整数 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·泸县月考) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·南山开学考) 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE=45°，那么∠BAF的大小为（　　）

A . 15° B . 10° C . 20° D . 25°

答案解析收藏纠错 + 选题
6. (2024九下·南山开学考) 中国高铁的飞速发展，已成为中国现代化建设的重要标志 $\text{[math]}$ 如图是高铁线路在转向处所设计的圆曲线 $\text{[math]}$ 即圆弧 $\text{[math]}$ ，高铁列车在转弯时的曲线起点为 $\text{[math]}$ ，曲线终点为 $\text{[math]}$ ，过点 $\text{[math]}$ ， $\text{[math]}$ 的两条切线相交于点 $\text{[math]}$ ，列车在从 $\text{[math]}$ 到 $\text{[math]}$ 行驶的过程中转角 $\text{[math]}$ 为 $\text{[math]}$ 若圆曲线的半径 $\text{[math]}$ ，则这段圆曲线 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·南山开学考) 如图，在直角坐标系中，菱形 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ， $\text{[math]}$ 将菱形 $\text{[math]}$ 沿 $\text{[math]}$ 轴向右平移 $\text{[math]}$ 个单位长度，再沿 $\text{[math]}$ 轴向下平移 $\text{[math]}$ 个单位长度，得到菱形 $\text{[math]}$ ，其中点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·南山开学考) 下列哪一个是假命题（）

A . 五边形外角和为 $\text{[math]}$ B . 切线垂直于经过切点的半径 C . $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称点为 $\text{[math]}$ D . 抛物线 $\text{[math]}$ 对称轴为直线 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·南山开学考) 已知反比例函数y= $\text{[math]}$ 在第一象限内的图象与一次函数y=-x+b的图象如图所示，则函数 $\text{[math]}$ 的图象可能为（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2024九下·南山开学考) 发动机的曲柄连杆将直线运动转化为圆周运动，图 $\text{[math]}$ 是发动机的实物剖面图，图 $\text{[math]}$ 是其示意图，图 $\text{[math]}$ 中，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上往复运动，推动点 $\text{[math]}$ 做圆周运动形成 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 表示曲柄连杆的两直杆，点 $\text{[math]}$ 、 $\text{[math]}$ 是直线 $\text{[math]}$ 与 $\text{[math]}$ 的交点；当点 $\text{[math]}$ 运动到 $\text{[math]}$ 时，点 $\text{[math]}$ 到达 $\text{[math]}$ ，当点 $\text{[math]}$ 运动到 $\text{[math]}$ 时，点 $\text{[math]}$ 到达 $\text{[math]}$ ；若 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论正确的是（）
$\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ 当 $\text{[math]}$ 与 $\text{[math]}$ 相切时， $\text{[math]}$ ； $\text{[math]}$ 当 $\text{[math]}$ 时， $\text{[math]}$ ．

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题

二、填空题：本题共5小题，每小题3分，共15分。

11. (2024·湖南模拟) 小明从《红星照耀中国》，《红岩》，《长征》，《钢铁是怎样炼成的》四本书中随机挑选一本，其中拿到《红星照耀中国》这本书的概率为．

答案解析收藏纠错 + 选题
12. (2024九下·南山开学考) 若 $\text{[math]}$ ， $\text{[math]}$ ，则代数式 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2024九上·成都月考) 如图，菱形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. (2024九下·南山开学考) 如图，在直角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 至 $\text{[math]}$ 的位置，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，且点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2024·明水模拟) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题：本题共7小题，共56分。解答应写出文字说明，证明过程或演算步骤。

16. (2024九下·南山开学考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2024九下·南山开学考) 为了启发学生的阅读自觉性，培养学生的学习毅力，学校决定开展“读书月”活动，对学生最喜欢的图书种类进行了一次抽样调查，所有图书分成五类：艺术、文学、科普、传记、其他 $\text{[math]}$ 根据调查结果绘制了两幅不完整的统计图 $\text{[math]}$ 每位同学必选且只选最喜欢的一类 $\text{[math]}$ ，根据图中提供的信息，解答下列问题：
1. （1）这次调查的学生共有名，喜欢“文学”类的学生有名；
2. （2）在扇形统计图中“科普”类所对应的圆心角的度数是 $\text{[math]}$ ， “其他”类所对应的百分比是；
3. （3）如果要在这五类图书中任选两类进行调查，恰好选到学生最喜欢的“文学”与“科普”的两类图书的概率是．
答案解析收藏纠错 + 选题
18. (2024九下·南山开学考) 图 $\text{[math]}$ 、图 $\text{[math]}$ 、图 $\text{[math]}$ 均是 $\text{[math]}$ 的正方形网格，每个小正方形的边长均为 $\text{[math]}$ ，每个小正方形的顶点称为格点 $\text{[math]}$ 点 $\text{[math]}$ 、 $\text{[math]}$ 均在格点上，只用无刻度的尺，分别在给定的网格中按下列要求作 $\text{[math]}$ ，点 $\text{[math]}$ 在格点上．
1. （1）在图 $\text{[math]}$ 中， $\text{[math]}$ 的面积为 $\text{[math]}$ ；
2. （2）在图 $\text{[math]}$ 中， $\text{[math]}$ 的面积为 $\text{[math]}$ ；
3. （3）在图 $\text{[math]}$ 中， $\text{[math]}$ 是面积为 $\text{[math]}$ 的钝角三角形．
答案解析收藏纠错 + 选题
19. (2024九下·南山开学考) 为研究某种化学试剂的挥发情况，某研究团队在两种不同的场景下做对比实验，收集了该试剂挥发过程中剩余质量 $\text{[math]}$ 克 $\text{[math]}$ 随时间 $\text{[math]}$ 分钟 $\text{[math]}$ 变化的数据 $\text{[math]}$ ，并分别绘制在直角坐标系中，如图所示．
1. （1）从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，选择适当的函数模型分别模拟两种场景下 $\text{[math]}$ 随 $\text{[math]}$ 变化的函数关系，并求出相应的函数表达式；
2. （2）查阅文献可知，该化学试剂发挥作用的最低质量为 $\text{[math]}$ 克 $\text{[math]}$ 在上述实验中，该化学试剂在哪种场景下发挥作用的时间更长？
答案解析收藏纠错 + 选题
20. (2024九下·南山开学考) 学科综合
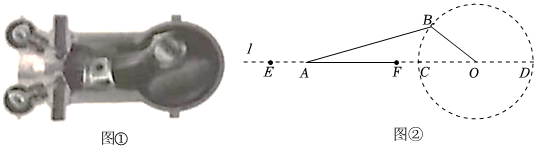
我们在物理学科中学过：光线从空气射入水中会发生折射现象 $\text{[math]}$ 如图 $\text{[math]}$ ，我们把 $\text{[math]}$ 称为折射率 $\text{[math]}$ 其中 $\text{[math]}$ 代表入射角， $\text{[math]}$ 代表折射角 $\text{[math]}$ ．
观察实验
为了观察光线的折射现象，设计了图 $\text{[math]}$ 所示的实验，即通过细管 $\text{[math]}$ 可以看见水底的物块 $\text{[math]}$ ，但不在细管 $\text{[math]}$ 所在直线上，图 $\text{[math]}$ 是实验的示意图，四边形 $\text{[math]}$ 为矩形，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，测得 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求入射角 $\text{[math]}$ 的度数．
2. （2）若 $\text{[math]}$ ，求光线从空气射入水中的折射率 $\text{[math]}$ 参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2024九下·南山开学考) 综合与实践
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆，车轮都是圆形的 $\text{[math]}$ 为什么车轮要做成圆形的呢？这里面有什么数学道理吗？带着这样的疑问，小青做了如下的探究活动：
将车轮设计成不同的正多边形，在水平地面上模拟行驶．
1. （1）探究一：将车轮设计成等边三角形，转动过程如图 $\text{[math]}$ ，设其中心到顶点的距离是 $\text{[math]}$ ，以车轮转动一次 $\text{[math]}$ 以一个顶点为支点旋转 $\text{[math]}$ 为例，中心的轨迹是 $\text{[math]}$ ， $\text{[math]}$ ，圆心角 $\text{[math]}$ 此时中心轨迹最高点是 $\text{[math]}$ 即 $\text{[math]}$ 的中点 $\text{[math]}$ ，转动一次前后中心的连线是 $\text{[math]}$ 水平线 $\text{[math]}$ ，请在图 $\text{[math]}$ 中计算 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ ．
2. （2）探究二：将车轮设计成正方形，转动过程如图 $\text{[math]}$ ，设其中心到顶点的距离是 $\text{[math]}$ ，以车轮转动一次 $\text{[math]}$ 以一个顶点为支点旋转 $\text{[math]}$ 为例，中心的轨迹是 $\text{[math]}$ ， $\text{[math]}$ ，圆心角 $\text{[math]}$ 此时中心轨迹最高点是 $\text{[math]}$ 即 $\text{[math]}$ 的中点 $\text{[math]}$ ，转动一次前后中心的连线是 $\text{[math]}$ 水平线 $\text{[math]}$ ，请在图 $\text{[math]}$ 中计算 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ 结果保留根号 $\text{[math]}$ ．
3. （3）探究三：将车轮设计成正六边形，转动过程如图 $\text{[math]}$ ，设其中心到顶点的距离是 $\text{[math]}$ ，以车轮转动一次 $\text{[math]}$ 以一个顶点为支点旋转 $\text{[math]}$ 为例，中心的轨迹是 $\text{[math]}$ ，圆心角 $\text{[math]}$ ．此时中心轨迹最高点是 $\text{[math]}$ 即 $\text{[math]}$ 的中点 $\text{[math]}$ ，转动一次前后中心的连线是 $\text{[math]}$ 水平线 $\text{[math]}$ ，在图 $\text{[math]}$ 中计算 $\text{[math]}$ 到 $\text{[math]}$ 的距离 $\text{[math]}$ $\text{[math]}$ 结果保留根号 $\text{[math]}$ ．
4. （4）归纳推理：比较 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 大小：，按此规律推理，车轮设计成的正多边形边数越多，其中心轨迹最高点与转动一次前后中心连线 $\text{[math]}$ 水平线 $\text{[math]}$ 的距离 $\text{[math]}$ 填“越大”或“越小” $\text{[math]}$ ．
5. （5）得出结论：将车轮设计成圆形，转动过程如图 $\text{[math]}$ ，其中心 $\text{[math]}$ 即圆心 $\text{[math]}$ 的轨迹与水平地面平行，此时中心轨迹最高点与转动前后中心连线 $\text{[math]}$ 水平线 $\text{[math]}$ 的距离 $\text{[math]}$ $\text{[math]}$ 这样车辆行驶平稳、没有颠簸感 $\text{[math]}$ 所以，将车轮设计成圆形．
答案解析收藏纠错 + 选题
22. (2024九下·南山开学考) $\text{[math]}$ 本小题 $\text{[math]}$ 分 $\text{[math]}$
探究函数 $\text{[math]}$ 的图象和性质，探究过程如下：
1. （1）自变量 $\text{[math]}$ 的取值范围是全体实数， $\text{[math]}$ 与 $\text{[math]}$ 的几组对应值列表如下：
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
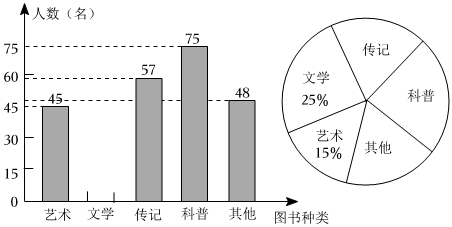
  其中， $\text{[math]}$ ▲ $\text{[math]}$ 根据如表数据，在图 $\text{[math]}$ 所示的平面直角坐标系中，通过描点画出了函数图象的一部分，请画出该函数图象的另一部分 $\text{[math]}$ 观察图象，写出该函数的一条性质；
2. （2）点 $\text{[math]}$ 是函数 $\text{[math]}$ 图象上的一动点，点 $\text{[math]}$ ，点 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出所有满足条件的点 $\text{[math]}$ 的坐标；
3. （3）在图 $\text{[math]}$ 中，当 $\text{[math]}$ 在一切实数范围内时，抛物线 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ ， $\text{[math]}$ 两点 $\text{[math]}$ 点 $\text{[math]}$ 在点 $\text{[math]}$ 的左边 $\text{[math]}$ ，点 $\text{[math]}$ 是点 $\text{[math]}$ 关于抛物线顶点的对称点，不平行 $\text{[math]}$ 轴的直线 $\text{[math]}$ 分别交线段 $\text{[math]}$ ， $\text{[math]}$ 不含端点 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点 $\text{[math]}$ 当直线 $\text{[math]}$ 与抛物线只有一个公共点时， $\text{[math]}$ 与 $\text{[math]}$ 的和是否为定值？若是，求出此定值；若不是，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

广东省深圳市南山实验教育集团麒麟中学2023-2024学年九...

副标题：

*注意事项：

广东省深圳市南山实验教育集团麒麟中学2023-2024学年九...

试题分析

总体分析

题量分析

难度分析

知识点分析

选手	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	平均成绩	中位数
成绩 $\text{[math]}$ 分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$