四川省广安市武胜县2023-2024学年九年级上学期数学期末...

更新时间：2024-05-14 浏览次数：17 类型：期末考试

一、选择题（本大题共10小题，每小题3分，共30分．每小题只有一个选项符合题意，请将所选选项填涂在答题卡上）

1. (2024九上·武胜期末) 二次函数 $\text{[math]}$ 的图像的开口方向是（）

A . 向左 B . 向右 C . 向上 D . 向下

答案解析收藏纠错 + 选题
2. (2024九上·武胜期末) 元至元四年（公元1267年），取“以武力胜南宋”之意，设置武胜军（与县同级），武胜县县名由此而来．下列数字图案中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九上·武胜期末) 若方程 $\text{[math]}$ 化为一元二次方程的一般形式后不含一次项，则 $\text{[math]}$ 的值为（）

A . 0 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九上·武胜期末) 同一平面内，已知 $\text{[math]}$ 的直径是 $\text{[math]}$ ，线段 $\text{[math]}$ ，则点 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是（）

A . 点 $\text{[math]}$ 在 $\text{[math]}$ 外 B . 点 $\text{[math]}$ 在 $\text{[math]}$ 上 C . 点 $\text{[math]}$ 在 $\text{[math]}$ 内 D . 不能确定

答案解析收藏纠错 + 选题
5. (2024九上·武胜期末) 事件“从一个只装有白球和红球的口袋中摸出一个球，这个球是黑球”是（）

A . 随机事件 B . 必然事件 C . 不可能事件 D . 无法确定

答案解析收藏纠错 + 选题
6. (2024九上·武胜期末) 若关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个实数根，则 $\text{[math]}$ 的值可以是（）

A . $\text{[math]}$ B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
7. (2024九上·武胜期末) 设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是抛物线 $\text{[math]}$ （m为常数）上的三点，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·武胜期末) 《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程符合题意的是（　　）

A . （x+2）²+（x﹣4）²＝x² B . （x﹣2）²+（x﹣4）²＝x² C . x²+（x﹣2）²＝（x﹣4）² D . （x﹣2）²+x²＝（x+4）²

答案解析收藏纠错 + 选题
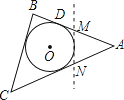
9. (2024九上·武胜期末) 如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，已知AD=10cm ，小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为（　　）

A . 20cm B . 15cm C . 10cm D . 随直线MN的变化而变化

答案解析收藏纠错 + 选题
10. (2024九上·武胜期末) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的一个交点为 $\text{[math]}$ ，与 $\text{[math]}$ 轴的交点 $\text{[math]}$ 在点 $\text{[math]}$ 与点 $\text{[math]}$ 之间（包含端点），顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③对于任意实数 $\text{[math]}$ ， $\text{[math]}$ 总成立；④关于 $\text{[math]}$ 的方程 $\text{[math]}$ 没有实数根.其中结论正确的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分．请将最简答案填写在答题卡相应位置）

11. (2024九上·武胜期末) 若方程 $\text{[math]}$ 的解是 $\text{[math]}$ ，则方程 $\text{[math]}$ 的解是 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024九上·武胜期末) 某水果公司购进 $\text{[math]}$ 岳池双鄢脐橙，希望出售这些脐橙能获得一定利润．在出售脐橙（去掉损坏的脐橙）时，需要先进行“脐橙损坏率”统计，再大约确定每千克脐橙的售价．如表是销售部通过随机取样，得到的“脐橙损坏率”统计表的一部分．估计这批脐橙损坏的概率为．（结果精确到 $\text{[math]}$ ）
脐橙总质量 $\text{[math]}$
250
300
350
450
500
损坏脐橙质量 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
脐橙损坏的频率 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

答案解析收藏纠错 + 选题
13. (2024九上·武胜期末) 若关于 $\text{[math]}$ 的函数 $\text{[math]}$ 的图象是抛物线，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
14. (2024九上·武胜期末) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，若 $\text{[math]}$ ，弦 $\text{[math]}$ 是 $\text{[math]}$ 内接正多边形的一边，则该正多边形的边数为．

答案解析收藏纠错 + 选题
15. (2024九上·武胜期末) 设 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
16. (2024九上·武胜期末) 如图，在平面直角坐标系中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ ，点 $\text{[math]}$ ．将矩形 $\text{[math]}$ 绕点A顺时针旋转，每次旋转 $\text{[math]}$ ，当第2023次旋转结束时，点 $\text{[math]}$ 的对应点的坐标是．

答案解析收藏纠错 + 选题

三、解答题（本大题共4小题．第17小题5分，第18、19、20小题各6分，共23分）

17. (2024九上·武胜期末) 按要求解方程：
1. （1） $\text{[math]}$ （配方法）；
2. （2） $\text{[math]}$ （因式分解法）．
答案解析收藏纠错 + 选题
18. (2024九上·武胜期末) 在平面直角坐标系中， $\text{[math]}$ 、线段 $\text{[math]}$ 和线段 $\text{[math]}$ 的位置如图所示．
1. （1）画出与 $\text{[math]}$ 关于原点 $\text{[math]}$ 对称的 $\text{[math]}$ ；
2. （2）线段 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转得到线段 $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ 的对应点分别为点 $\text{[math]}$ ， $\text{[math]}$ ），作出旋转中心点 $\text{[math]}$ ．（保留作图痕迹，不写作法）
答案解析收藏纠错 + 选题
19. (2024九上·武胜期末) 如图，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接四边形， $\text{[math]}$ 是等边三角形， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
20. (2024九下·凉州模拟) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上两点， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 后得到 $\text{[math]}$ ，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

四、实践应用题（本大题共4小题．第21小题6分，第22、23、24小题各8分，共30分）

21. (2024九上·武胜期末) $\text{[math]}$ 于8月29日上市，该系列完成了核心技术领域从0到1的跃迁，让无数国人为之自豪并被赞誉为“争气机”，手机背面有一条圆弧，象征着以山河之美致敬奔腾不息的力量，圆孤对应的弦 $\text{[math]}$ 长 $\text{[math]}$ ，弓形高 $\text{[math]}$ 长 $\text{[math]}$ 求半径 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
22. (2024九上·武胜期末) 班级团队建设联欢晚会时，在教室悬挂了如图所示的四个灯笼 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．晚会结束后，小明摘下了两个灯笼（剩两个灯笼未摘），他每次随机摘下一个灯笼，且摘 $\text{[math]}$ 之前需先摘下 $\text{[math]}$ ，摘 $\text{[math]}$ 之前需先摘下 $\text{[math]}$ ．
1. （1）小明第一个摘下的灯笼是 $\text{[math]}$ 灯笼的概率是；
2. （2）求小明第二个摘下的灯笼是 $\text{[math]}$ 灯笼的概率．
答案解析收藏纠错 + 选题
23. 小林同学不仅是一名羽毛球运动爱好者，还喜欢运用数学知识对羽毛球比赛进行技术分析，下面是他对击球线路的分析．
如图，在平面直角坐标系中，点A，C在x轴上，球网AB与y轴的水平距离 $\text{[math]}$ m， $\text{[math]}$ m，击球点P在y轴上．若选择扣球，羽毛球的飞行高度y（m）与水平距离x（m）近似满足一次函数关系 $\text{[math]}$ ；若选择吊球，羽毛球的飞行高度y（m）与水平距离x（m）近似满足二次函数关系 $\text{[math]}$ ．
1. （1）求点P的坐标和a的值．
2. （2）小林分析发现，上面两种击球方式均能使球过网．要使球的落地点到C点的距离更近，请通过计算判断应选择哪种击球方式．
答案解析收藏纠错 + 选题
24. (2024九上·武胜期末) 由于新冠疫情的影响，口罩需求量急剧上升，经过连续两次价格的上调，口罩的价格由每包10元涨到了每包16.9元.
1. （1）求出这两次价格上调的平均增长率；
2. （2）在有关部门大力调控下，口罩价格还是降到了每包10元，而且调查发现，定价为每包10元时，一天可以卖出30包，每降价1元，可以多卖出5包.当销售额为315元时，且让顾客获得更大的优惠，应该降价多少元？
答案解析收藏纠错 + 选题

五、推理论证题（9分）

25. (2024九上·武胜期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以直角边 $\text{[math]}$ 为直径的 $\text{[math]}$ 交斜边 $\text{[math]}$ 于点 $\text{[math]}$ ．点 $\text{[math]}$ 为边 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求证：直线 $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 的半径为2，求阴影部分的面积．
答案解析收藏纠错 + 选题

六、拓展探究题（10分）

26. (2024九上·武胜期末) 如图1，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点B和C ，点B在x轴上，点C在y轴上，抛物线与x轴的另一个交点为A ．
1. （1）求抛物线 $\text{[math]}$ 的解析式；
2. （2）如图2，点P为直线 $\text{[math]}$ 上方抛物线上一动点， $\text{[math]}$ 于点D ， $\text{[math]}$ 轴于点F ，交 $\text{[math]}$ 于点E ，求 $\text{[math]}$ 周长的最大值以及点P的坐标；
3. （3）在（2）的结论下，将抛物线 $\text{[math]}$ 沿射线 $\text{[math]}$ 方向平移 $\text{[math]}$ 个单位长度得到新抛物线 $\text{[math]}$ ，新抛物线的顶点为M ，平面内有一点N ，以点P、B、M、N为顶点的四边形是平行四边形，直接写出点N的坐标．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

四川省广安市武胜县2023-2024学年九年级上学期数学期末...

副标题：

*注意事项：

四川省广安市武胜县2023-2024学年九年级上学期数学期末...

试题分析

总体分析

题量分析

难度分析

知识点分析

脐橙总质量 $\text{[math]}$	250	300	350	450	500
损坏脐橙质量 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
脐橙损坏的频率 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$