一、选择题(本大题共12小题,每小题3分,共36分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
-
-
-
3.
(2024七下·金沙月考)
如图,直线公路l上共有A、B、C、D四个核酸检测点,若从点M用相同速度到任意一个核酸检测点,用时最短的路径是( )
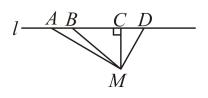
-
4.
(2024七下·金沙月考)
据悉,毕节市今年的油菜计划种植任务是103.84万亩,其中金沙、黔西、织金属于油菜生产重点县(市).已知一粒油菜籽的质量约为0.0000015

. 数据0.0000015用科学记数法表示为( )
-
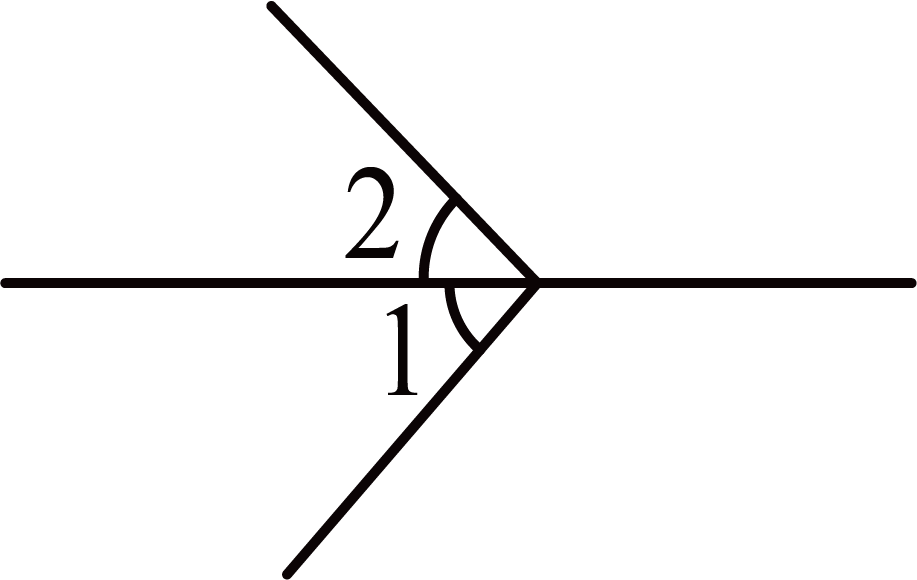
A . ∠1
B . ∠2
C . ∠3
D . ∠4
-
6.
(2024七下·金沙月考)
如图,利用1个边长为

的大正方形的面积

个边长为
a的小正方形的面积

个邻边长分别为
a ,
b的长方形的面积

个边长为
b的小正方形的面积,即可说明完全平方公式,这里体现的数学思想是( )
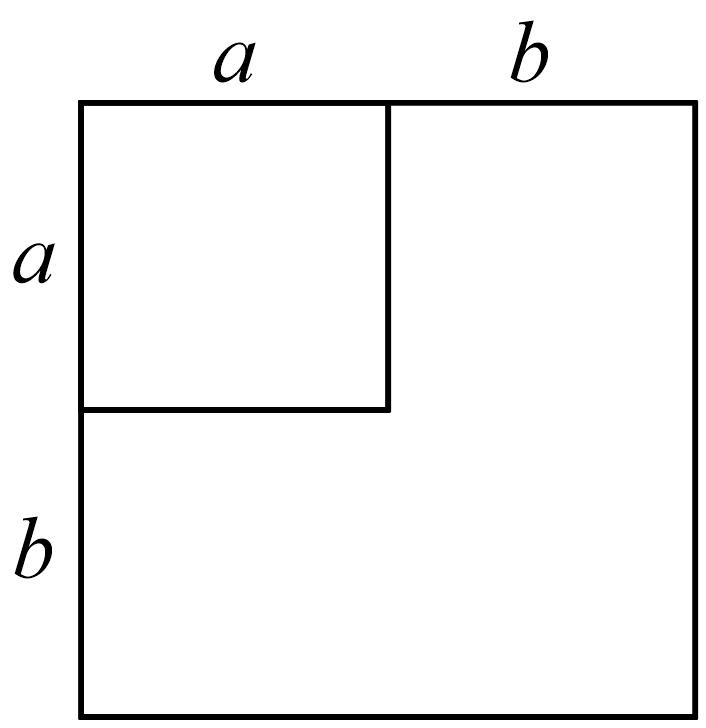
A . 数形结合思想
B . 类比思想
C . 整体思想
D . 分类讨论思想
-
-
A .  B . 1
C .
B . 1
C .  D . 2
D . 2
-
-
10.
(2024七下·金沙月考)
从前,古希腊一位庄园主把一块边长为
a米(

)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加10米,相邻的另一边减少10米,变成一个长方形的土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A . 变小了
B . 变大了
C . 没有变化
D . 无法确定
-
-
12.
(2024七下·金沙月考)
如图,图①所示的小长方形两条边的长分别为1,
m(
m>1),现将这样5个大小形状完全相同的小长方形不重叠地放入图②所示的大长方形中,图中未被覆盖部分用阴影表示,其面积分别为
S1 ,
S2 . 设面积为
S1的长方形一条边为
x . 若无论
x为何值,图中阴影部分
S1﹣
S2的值总保持不变,此时
S1﹣
S2的值为( )
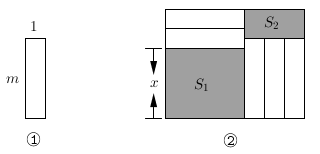
A .  B . 2
C .
B . 2
C .  D . 3
D . 3
二、填空题(本大题共4小题,每小题4分,共16分)
-
-
14.
(2024七下·金沙月考)
如图是小明探索直线平行的条件时所用的学具,木条
a ,
b ,
c在同一平面内.经测量

, 要使木条

, 则

的度数应为
.

-
-
16.
(2024七下·金沙月考)
将一块三角板

(

,

)按如图所示方式放置,使
A ,
B两点分别落在直线
m ,
n上,下列三个条件:①

;②

,

;③

. 其中能判断直线


的有
.(填序号)

三、解答题(本大题共9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤)
-
-
(1)

;
-
(2)

.
-
-
-
-
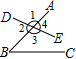
(1)
写出

的所有邻补角:
;
-
(2)
若

, 求

的度数.
-
-
22.
(2024七下·金沙月考)
如图,在台球运动中(每次撞击桌边时,撞击前后的路线与桌边所成的夹角相等),如果母球
P击中桌边点
A , 经桌边反弹后击中相邻的另一桌边点
B , 然后又反弹击中球
C .

-
(1)
若

, 求

的度数.
-
(2)
母球
P经过的路线

与

一定平行吗?请说明理由.
-
-
-
(2)
求代数式

的值.
-
-
(1)
【基础应用】①已知

,

, 则

的值为
;
②若x满足 , 求
, 求 的值.
的值.
-
(2)
【拓展应用】如图,某学校有一块梯形空地

,

于点
E ,

,

, 该校计划在三角形

和三角形

区域内种花,在剩余区域内种草,经测量,种花区域的面积和为

,

, 求种草区域的面积和.
-
25.
(2024七下·金沙月考)
在四边形

中,

,

和

的角平分线或邻补角角平分线分别为

和

.
如图1,当 ,
,  都为角平分线时,小明发现
都为角平分线时,小明发现 , 并给出下面的理由:
, 并给出下面的理由:
解:∵ ,
,  ,
,  ,
,  ,
,
∴ ,
,
∴ .
.
又∵ ,
,  ,
,
∴ ,
,
∴ ,
,
∴ .
.
根据小明的发现,解决下面的问题:
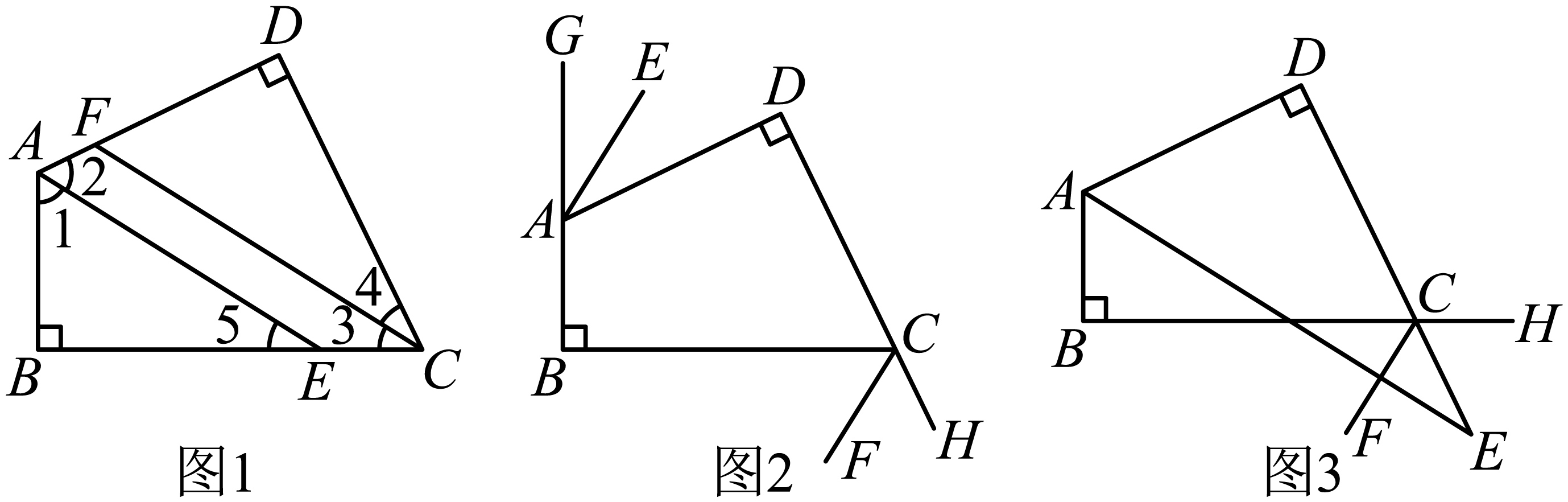
-
(1)
如图2,当

,

都为邻补角的角平分线时,

与

的位置关系是什么?并给出理由.
-
(2)
如图3,当

是角平分线,

是邻补角的角平分线时,请你探索

与

的位置关系,并给出理由.(提示:两直线平行,内错角相等)
 B .
B .  C .
C . 




, 求
的值.
,
都为角平分线时,小明发现
, 并给出下面的理由:
,
,
,
,
,
.
,
,
,
,
.
