广西南宁市马山县周鹿中学2023-2024学年高一下学期期中...

更新时间：2024-05-14 浏览次数：28 类型：期中考试

一、选择题：本题共8小题，每小题5分，共40分。每小题只有一个选项符合题目要求。

1. (2024高一下·马山期中) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·马山期中) 已知幂函数 $\text{[math]}$ 的图象过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 9 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一下·马山期中) 设函数 $\text{[math]}$ ( $\text{[math]}$ ， $\text{[math]}$ 是常数， $\text{[math]}$ ， $\text{[math]}$ ).若 $\text{[math]}$ 在区间 $\text{[math]}$ 上具有单调性，且 $\text{[math]}$ ，则( )

A . $\text{[math]}$ 的周期为 $\text{[math]}$ B . $\text{[math]}$ 的单调递减区间为 $\text{[math]}$ C . $\text{[math]}$ 的图象与 $\text{[math]}$ 的图象重合 D . $\text{[math]}$ 的对称轴为 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一下·马山期中) 在 $\text{[math]}$ 中，D为 $\text{[math]}$ 的中点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点G， $\text{[math]}$ ，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·马山期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，点P是线段 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，则点P的坐标是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一下·马山期中) 设 $\text{[math]}$ ，则复数z的实部和虚部之和为( )

A . 3 B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·马山期中) 已知直三棱柱 $\text{[math]}$ 的侧棱长为2， $\text{[math]}$ ， $\text{[math]}$ .过AB， $\text{[math]}$ 的中点E，F作平面 $\text{[math]}$ 与平面 $\text{[math]}$ 垂直，则平面 $\text{[math]}$ 截该三棱柱所得截面的周长为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一下·马山期中) 梯形ABCD，上底 $\text{[math]}$ ，腰 $\text{[math]}$ ，下底 $\text{[math]}$ ，以下底所在直线为x轴，则由斜二侧画法画出的直观图 $\text{[math]}$ 的面积为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题

二、多项选择题：本题共4小题，每小题5分，共20分。每小题有多个选项符合题目要求，全部选对得5分，部分选对得2分，有错选得0分。

9. (2024高一下·马山期中) 已知函数 $\text{[math]}$ 的相邻对称轴之间的距离为 $\text{[math]}$ ，且 $\text{[math]}$ 图象经过点 $\text{[math]}$ ，则下列说法正确的是（）

A . 该函数解析式为 $\text{[math]}$ B . 函数 $\text{[math]}$ 的一个对称中心为 $\text{[math]}$ C . 函数 $\text{[math]}$ 的定义域为 $\text{[math]}$ D . 将函数 $\text{[math]}$ 的图象向右平移 $\text{[math]}$ 个单位，得到函数 $\text{[math]}$ 的图象，且函数 $\text{[math]}$ 的图象关于原点对称，则b的最小值为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2024高一下·马山期中) 有下列说法，其中正确的说法为（）

A . 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则P是三角形 $\text{[math]}$ 的垂心 C . 两个非零向量 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 共线且反向 D . 若 $\text{[math]}$ ，则存在唯一实数 $\text{[math]}$ 使得 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一下·马山期中) 对任意复数 $\text{[math]}$ ， $\text{[math]}$ ，定义 $\text{[math]}$ ，其中 $\text{[math]}$ 是 $\text{[math]}$ 的共轭复数，对任意复数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，下列命题为真命题的是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高一下·龙马潭期中) 已知AC为圆锥SO底面圆O的直径（S为顶点，O为圆心），点B为圆O上异于A，C的动点， $\text{[math]}$ ， $\text{[math]}$ 则下列结论正确的为( )

A . 圆锥SO的侧面积为 $\text{[math]}$ B . $\text{[math]}$ 的取值范围为 $\text{[math]}$ C . 若 $\text{[math]}$ ， E为线段AB上的动点，则 $\text{[math]}$ D . 过该圆锥顶点S的平面截此圆锥所得截面面积的最大值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分。

13. (2024高一下·马山期中) 命题： $\text{[math]}$ ， $\text{[math]}$ 的否定为真命题，则实数a的最大值为.

答案解析收藏纠错 + 选题
14. (2024高一下·马山期中) 已知单位向量 $\text{[math]}$ 满足 $\text{[math]}$ ，则m的范围是.

答案解析收藏纠错 + 选题
15. (2024高一下·马山期中) 在复平面内，等腰直角三角形 $\text{[math]}$ 以 $\text{[math]}$ 为斜边（其中O为坐标原点），若 $\text{[math]}$ 对应的复数 $\text{[math]}$ ，则直角顶点 $\text{[math]}$ 对应的复数 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2024高一下·马山期中) n为不超过1996的正整数，如果有一个θ，使（sinθ+icosθ）ⁿ=sinnθ+icosnθ成立，则满足上述条件的n值共有个.

答案解析收藏纠错 + 选题

四、解答题：本题共6小题，共70分。解答应写出必要得文字说明，证明过程或演算步骤。

17. (2024高一下·马山期中) 设函数 $\text{[math]}$ ．
1. （1）设 $\text{[math]}$ ，求函数 $\text{[math]}$ 的最大值和最小值；
2. （2）设函数 $\text{[math]}$ 为偶函数，求 $\text{[math]}$ 的值，并求函数 $\text{[math]}$ 的单调增区间．
答案解析收藏纠错 + 选题
18. (2024高一下·马山期中) 如图，在梯形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2024高一下·马山期中) 已知复数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）若复数 $\text{[math]}$ 在复平面内的对应点落在第二象限，求实数a的取值范围；
2. （2）若虚数 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根，求实数m的值.
答案解析收藏纠错 + 选题
20. (2024高一下·马山期中) 若圆锥底面半径为 $\text{[math]}$ ，高为 $\text{[math]}$ ，其中有一个内接正方体，求这个内接正方体的棱长.

答案解析收藏纠错 + 选题
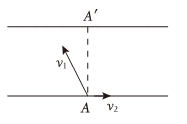
21. (2024高一下·马山期中) 一条河南北两岸平行.如图所示，河面宽度 $\text{[math]}$ ，一艘游船从南岸码头A点出发航行到北岸.游船在静水中的航行速度是 $\text{[math]}$ ，水流速度 $\text{[math]}$ 的大小为 $\text{[math]}$ .设 $\text{[math]}$ 和 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，北岸上的点 $\text{[math]}$ 在点A的正北方向.
1. （1）若游船沿 $\text{[math]}$ 到达北岸 $\text{[math]}$ 点所需时间为 $\text{[math]}$ ，求 $\text{[math]}$ 的大小和 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ 时，游船航行到北岸的实际航程是多少？
答案解析收藏纠错 + 选题
22. (2024高一下·马山期中) 已知 $\text{[math]}$ 是关于x的实系数一元二次方程.
1. （1）若a是方程的一个根，且 $\text{[math]}$ ，求实数k的值；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 是该方程的两个实根，且 $\text{[math]}$ ，求使 $\text{[math]}$ 的值为整数的所有k的值.
答案解析收藏纠错 + 选题