浙江省宁波市海曙区2022-2023学年七年级下学期期中数学...

更新时间：2024-05-10 浏览次数：17 类型：期中考试

一、选择题（每小题3分，共30分）

1. (2023七下·海曙期中) 仔细观察下列图形，其中∠1与∠2是内错角的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023七下·海曙期中) 下列方程中，属于二元一次方程的是（　　）

A . 2x﹣y＝0 B . x+y﹣z＝0 C . 2x﹣3＝0 D . x $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·海曙期中) 下列计算正确的是（　　）

A . 2m²•3m³＝6m B . m•m⁵＝（﹣m³）² C . （﹣3mn）³＝﹣9m³n D . （﹣2mn²）²＝4m²n²

答案解析收藏纠错 + 选题
4. (2023七下·海曙期中) 下列等式中，从左到右的变形属于因式分解的是（　　）

A . x+2y＝（x+y）+y B . p（q+h）＝pq+ph C . 4a²﹣4a+1＝4a（a﹣1）+1 D . 5x²y﹣10xy²＝5xy（x﹣2y）

答案解析收藏纠错 + 选题
5. (2023七下·海曙期中) 一种花粉颗粒直径约为0.0000065米，数字0.0000065用科学记数法表示为（　　）

A . 0.65×10^﹣5 B . 6.5×10^﹣6 C . 6.5×10⁶ D . 6.5×10⁵

答案解析收藏纠错 + 选题
6. (2023七下·海曙期中) 若s+t＝4，则s²﹣t²+8t的值是（　　）

A . 8 B . 12 C . 16 D . 32

答案解析收藏纠错 + 选题
7. (2023七下·海曙期中) 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+3b），宽为（a+2b）的大长方形，则需要A类、B类和C类卡片的张数分别为（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·海曙期中) 若（x﹣2）（x²﹣mx+1）的展开式中不含x的二次项，则化简后的一次项系数是（　　）

A . ﹣3 B . ﹣2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023七下·海曙期中) 若m，n均是正整数，且2^m+1×4ⁿ=128，则m+n的所有可能值为（）

A . 5或4 B . 3或4 C . 2或3 D . 6或5

答案解析收藏纠错 + 选题
10. (2023七下·海曙期中) 如图，AB∥CD ，点P在AB ， CD之间，∠ACP＝2∠PCD＝40°，连结AP ，若∠BAP=α，∠CAP＝α+β.下列说法中正确的是（）

A . 当∠P＝60°时，α＝30° B . 当∠P＝60°时，β＝40° C . 当β＝20°时，∠P＝90° D . 当β＝0°时，∠P＝90°

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共18分）

11. (2023七下·海曙期中) 计算：（﹣2）²⁰²³×（ $\text{[math]}$ ）²⁰²³＝．

答案解析收藏纠错 + 选题
12. (2023七下·海曙期中) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2023七下·海曙期中) 将4x﹣3y＝5变形成含x的代数式表示y ，则y＝．

答案解析收藏纠错 + 选题
14. (2023七下·海曙期中) 如果多项式4x²﹣（1﹣m）x+9是一个完全平方式，则常数m的值是．

答案解析收藏纠错 + 选题
15. (2023七下·海曙期中) 已知关于x ， y的二元一次方程组 $\text{[math]}$ 有下列说法：①当x与y相等时，解得k＝﹣4；②当x与y互为相反数时，解得k＝3；③若4^x•8^y＝32，则k＝11；④无论k为何值，x与y的值一定满足关系式x+5y+12＝0．其中正确的序号是．

答案解析收藏纠错 + 选题
16. (2024七下·慈利期中) 如图有两张正方形纸片A和B，图1将B放置在A内部，测得阴影部分面积为3；图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为21；若将3个正方形A和2个正方形B并列放置后构造新正方形如图3 (图2，图3中正方形AB纸片均无重叠部分)，则图3阴影部分面积是

答案解析收藏纠错 + 选题

三、解答题（第17-22题，每小题6分，第23、24题，每小题6分，共52分）

17. (2023七下·海曙期中) 分解因式
1. （1） x²y﹣y；
2. （2） ax²﹣6ax+9a ．
答案解析收藏纠错 + 选题
18. (2023七下·海曙期中) 解方程组：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2023七下·海曙期中) 计算：
1. （1）（﹣1）²⁰²³﹣（ $\text{[math]}$ ）⁰；
2. （2）（15x³y⁵﹣10x³y⁴﹣20x³y²）÷（﹣5x³y²）．
答案解析收藏纠错 + 选题
20. (2023七下·海曙期中) 先化简，再求值：（x﹣2）（3x²﹣1）﹣12x（ $\text{[math]}$ x² $\text{[math]}$ x﹣3），其中x $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2023七下·海曙期中) 如图所示，有一块长宽为（3a+b）米和（a+2b）米的长方形土地，现准备在这块土地上修建一个长为（2a+b）米，宽为（a+b）米的游泳池，剩余部分修建成休息区域．
1. （1）请用含a和b的代数式表示休息区域的面积；（结果要化简）
2. （2）若a＝5，b＝10，求休息区域的面积．
答案解析收藏纠错 + 选题
22. (2023七下·海曙期中) 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具，据了解，8只“冰墩墩”和10只“雪容融”的进价共计2000元；10只“冰墩墩”和20只“雪容融”的进价共计3100元．
1. （1）求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元；
2. （2）该专卖店计划恰好用3500元购进“冰墩墩”和“雪容融”两种毛绒玩具（两种均购买），求专卖店共有几种采购方案．
答案解析收藏纠错 + 选题
23. (2023七下·海曙期中)
1. （1）问题发现：
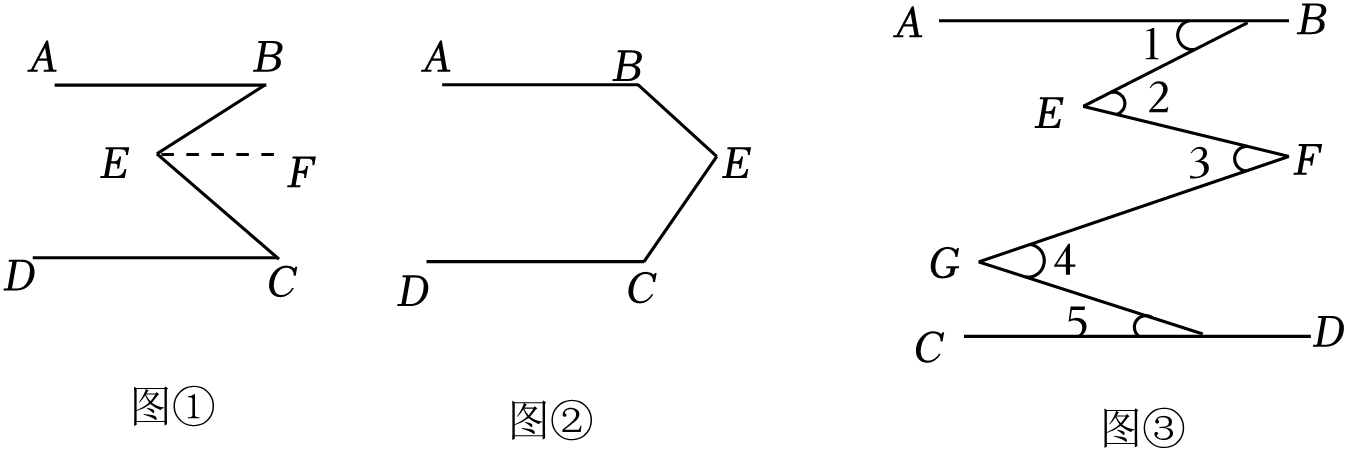
  如图①，直线AB∥CD ，连接BE ， CE ，可以发现∠B+∠C＝∠BEC ，请把下面的证明过程补充完整：
  证明：过点E作EF∥AB ，
  ∵AB∥DC（已知）
  ∴EF∥DC（）．
  ∴∠C＝∠CEF ．（）．
  ∵EF∥AB ，
  ∴∠B＝∠BEF （同理）．
  ∴∠B+∠C＝（等量代换），即∠B+∠C＝∠BEC ．
2. （2）拓展探究：
  如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C+∠BEC＝360°．
3. （3）解决问题：如图③，AB∥DC ， E、F、G是AB与CD之间的点，直接写出∠1，∠2，∠3，∠4，∠5之间的数量关系．
答案解析收藏纠错 + 选题
24. (2023七下·海曙期中) 【学习材料】拆项添项法
在对某些多项式进行因式分解时，需要把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符号相反的项，这样的分解因式的方法称为拆项添项法，如：
例1：分解因式：x⁴+4y⁴
解：原式＝x⁴+4y⁴＝x⁴+4x²y²+4y⁴﹣4x²y²
＝（x²+2y²）²﹣4x²y²＝（x²+2y²+2xy）（x²+2y²﹣2xy）
例2：分解因式：x³+5x﹣6
解：原式＝x³﹣x+6x﹣6＝x（x²﹣1）+6（x﹣1）＝（x﹣1）（x²+x+6）
我们还可以通过拆项对多项式进行变形，如
例3、把多项式a²+b²+4a﹣6b+13写成A²+B²的形式．
解：原式＝a²+4a+4+b²﹣6b+9＝（a+2）²+（b﹣3）²
【知识应用】请根据以上材料中的方法，解决下列问题：
1. （1）分解因式：x²+2x﹣8＝；
2. （2）分解因式：x⁴+4＝；
3. （3）关于x的二次三项式x²﹣20x+111在x＝时，有最小值；
4. （4）已知M＝x²+6x+4y²﹣12y+m（x ， y均为整数，m是常数），若M恰能表示成A²+B²的形式，求m的值．
答案解析收藏纠错 + 选题