一、选择题(本大题共10小题,每小题3分,共30分,在每小题的四个选项中,只有一项正确)
-
1.
(2024八下·南海月考)
剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕、年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中,是轴对称图形,但不是中心对称图形的是( )
-
2.
(2024八下·南海月考)
某商场的货运电梯只限载货,严禁载人.根据如图所示的标识,货梯运送货物的质量

满足的不等关系是( )


-
-
-
5.
(2024八下·南海月考)
如图,

是由

通过平移得到,且点
B ,
E ,
C ,
F在同一条直线上.若

, 则
BE的长度是( )

A . 1
B . 2
C . 3
D . 4
-
A . 2
B .  C . 4
D .
C . 4
D . 
-
-
8.
(2024八下·南海月考)
如图,
A、
B、
C三个居民小区的位置成三角形,为了大家的生活便利,现决定三个小区之间修建一个超市,使它到三个小区的距离相等,则超市应建在( )

A . AC、BC的两条高线的交点处
B . 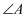 /
/ 两内角角平分线的交点处
C . AC、BC两边中线的交点处
D . AC、BC两条边垂直平分线的交点处
两内角角平分线的交点处
C . AC、BC两边中线的交点处
D . AC、BC两条边垂直平分线的交点处
-
9.
(2024八下·南海月考)
小明将两把完全相同的长方形直尺如图放置在

上,两把直尺的接触点为
P , 则射线
OP , 即为

的角平分线.边
OA与其中一把直尺边缘的交点为
C , 点
C、
P在这把直尺上的刻度读数分别是2、5,则
OC的长度是( )

A .  B . 2.5
C .
B . 2.5
C .  D . 3
D . 3
-
A . 6
B .  C .
C .  D . 9
D . 9
二、填空题(本大题共5小题,每小题3分,共15分)
-
-
-
-
-
15.
(2024八下·南海月考)
如图,已知△ABC中,∠ACB=90°,∠BAC=30°,BC=2,AB=4,AC=2

, 点D为直线AB上一动点,将线段CD绕点C顺时针旋转60°得到线段CE,连接ED、BE,点F在直线AF上且DF=BC,则BE最小值为
.

三、解答题(一)(本大题共3小题,每小题8分,共24分)
-
-
17.
(2024八下·南海月考)
如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,

的顶点都在格点上.

-
-
(2)
画出

关于点
O的中心对称图形

.
-
-
(1)
若

的面积是20,且

, 求
AD的长;
-
(2)
若

, 求

的度数.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
-
-
(1)
求证:

;
-
(2)
若

,

, 求
AE的长.
-
20.
(2024八下·南海月考)
近年来,桂城坚定不移发展教育事业,始终保障促进教育高质量发展,不断加快新改扩建学校工程建设,推进桂城教育现代化.为了提高学生的精神生活,绿化校园,美化校园环境,将要购进
A、
B两个品种的树苗,已知一株
A品种树苗比一株
B品种树苗多20元,若买一株
A品种树苗和2株
B品种树苗共需110元.
-
-
(2)
学校若花费不超过4000元购入A、B两种树苗,已知A品种树苗数量是B品种树苗数量的一半,问此次至多购买B品种树苗多少株?
-
21.
(2024八下·南海月考)
在边长为9的等边三角形
ABC中,点
P是
AB上一动点,以每秒1个单位长度的速度从点
A向点
B运动,设运动时间为
t秒.

-
(1)
如图1,若点
Q是
BC上一定点,

,

, 求
t的值;
-
(2)
如图2,若点
P从点
A向点
B运动,同时点
Q以每秒2个单位长度的速度从点
B先向点
C再向点
A运动,当
t为何值时,

为等边三角形?
五、解答题(三)(本大题共2小题,每小题12分,共24分)
-
22.
(2024八下·南海月考)
定义:如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的“相伴方程”,例如:方程

的解为

, 不等式组

的解为

, 因为

, 所以称方程

为不等式组

的“相伴方程”.
-
(1)
下列方程是不等式组

的“相伴方程”的是
;(填序号)
① ;②
;② ;③
;③ .
.
-
(2)
若关于
x的方程

是不等式组

0的“相伴方程”,求
k的取值范围;
-
(3)
若方程

,

都是关于
x的不等式组

的“相伴方程”,其中

, 求
m的取值范围.
-
23.
(2024八下·南海月考)
综合与实践,问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知

中,

,

. 将

从图1的位置开始绕点
A逆时针旋转,得到

(点
D ,
E分别是点
B ,
C的对应点),旋转角为

, 设线段
AD与
BC相交于点
M , 线段
DE分别交
BC ,
AC于点
O ,
N .

-
(1)
特例分析:如图2,当旋转到

时,判断

的形状并说明理由;
-
(2)
探究规律:如图3,在

绕点
A逆时针旋转过程中,“求真”小组的同学发现线段
DM始终等于线段
CN , 请你证明这一结论;
-
(3)
拓展延伸:①请求出当

是等腰三角形时旋转角

的度数;
②在图3中,作直线BD , CE交于点P , 直接写出当 时旋转角
时旋转角 的度数.
的度数.
 B .
B .  C .
C .  D .
D . 




;②
;③
.

时旋转角
的度数.