广东省深圳市宝安区宝安中学2023-2024学年高二（下）月...

更新时间：2024-05-17 浏览次数：18 类型：月考试卷

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1. (2024高二下·宝安月考) 已知曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线与直线 $\text{[math]}$ 垂直，则 $\text{[math]}$ 点的坐标为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二下·宝安月考) 在棱长为 $\text{[math]}$ 的正方体 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的中点，则点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二下·宝安月考) 已知函数 $\text{[math]}$ 的图象如图所示，则不等式 $\text{[math]}$ 的解集为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二下·宝安月考) 设点 $\text{[math]}$ 是函数 $\text{[math]}$ 图象上的任意一点，点 $\text{[math]}$ 处切线的倾斜角为 $\text{[math]}$ ，则角 $\text{[math]}$ 的取值范围是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二下·惠州月考) 从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，任取两个不同的数作对数的底数和真数，则所有不同的对数的值有( )

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题
6. (2024高二下·宝安月考) 若函数 $\text{[math]}$ 存在 $\text{[math]}$ 个极值点，则称 $\text{[math]}$ 为 $\text{[math]}$ 折函数，例如 $\text{[math]}$ 为 $\text{[math]}$ 折函数，已知函数 $\text{[math]}$ ，则 $\text{[math]}$ 为( )

A . $\text{[math]}$ 折函数 B . $\text{[math]}$ 折函数 C . $\text{[math]}$ 折函数 D . $\text{[math]}$ 折函数

答案解析收藏纠错 + 选题
7. (2024高二下·宝安月考) 已知 $\text{[math]}$ ， $\text{[math]}$ 为圆 $\text{[math]}$ ： $\text{[math]}$ 上两点，且 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ ： $\text{[math]}$ 上，则 $\text{[math]}$ 的最小值为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·遂宁月考) 已知函数 $\text{[math]}$ ，若总存在两条不同的直线与函数 $\text{[math]}$ ， $\text{[math]}$ 图象均相切，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。

9. (2024高二下·宝安月考) 设数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ， $\text{[math]}$ ，则下列说法正确的是( )

A . $\text{[math]}$ 是等差数列 B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等差数列，公差为 $\text{[math]}$ C . 当 $\text{[math]}$ 或 $\text{[math]}$ 时， $\text{[math]}$ 取得最大值 D . $\text{[math]}$ 时， $\text{[math]}$ 的最大值为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二下·宝安月考) 已知 $\text{[math]}$ ， $\text{[math]}$ 分别是椭圆 $\text{[math]}$ ： $\text{[math]}$ 的左、右焦点，如图，过 $\text{[math]}$ 的直线与 $\text{[math]}$ 交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ 的离心率为 $\text{[math]}$ ，则( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二下·宝安月考) 已知函数 $\text{[math]}$ ，则下列结论正确的是( )

A . 函数 $\text{[math]}$ 存在三个不同的零点 B . 函数 $\text{[math]}$ 既存在极大值又存在极小值 C . 若 $\text{[math]}$ 时， $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为 $\text{[math]}$ D . 当 $\text{[math]}$ 时，方程 $\text{[math]}$ 有且只有两个实根

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分。

12. (2024高二下·宝安月考) 若函数 $\text{[math]}$ 在 $\text{[math]}$ 上的最小值为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
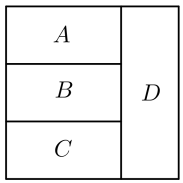
13. (2024高二下·广西期末) 如图，用4种不同的颜色对图中4个区域涂色，要求每个区域涂1种颜色，相邻的区域不能涂相同的颜色，则不同的涂色方法有种．

答案解析收藏纠错 + 选题
14. (2024高二下·宝安月考) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，都有 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。

15. (2024高二下·宝安月考) 已知函数 $\text{[math]}$ ．
1. （1）求曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线与两坐标轴围成的三角形面积；
2. （2）过点 $\text{[math]}$ 作曲线 $\text{[math]}$ 的切线，若切线有且仅有 $\text{[math]}$ 条，求实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
16. (2024高二下·宝安月考) 已知双曲线 $\text{[math]}$ ： $\text{[math]}$ 过点 $\text{[math]}$ ，且与双曲线 $\text{[math]}$ ： $\text{[math]}$ 有相同的渐近线．
1. （1）求双曲线 $\text{[math]}$ 的方程；
2. （2）若直线 $\text{[math]}$ ： $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，且线段 $\text{[math]}$ 的垂直平分线过点 $\text{[math]}$ ，求直线 $\text{[math]}$ 的方程．
答案解析收藏纠错 + 选题
17. (2024高二下·宝安月考) 如图，已知三棱柱 $\text{[math]}$ 的侧棱与底面垂直， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上动点且 $\text{[math]}$ 恒成立．
1. （1）证明： $\text{[math]}$ ；
2. （2）当三棱锥 $\text{[math]}$ 与三棱锥 $\text{[math]}$ 的体积之和为 $\text{[math]}$ 时，求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的余弦值．
答案解析收藏纠错 + 选题
18. (2024高二下·宝安月考) 若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造出新的数列 $\text{[math]}$ 现对数列 $\text{[math]}$ ， $\text{[math]}$ 进行构造，第一次得到数列 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；第二次得到数列 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；依次构造，第 $\text{[math]}$ 次得到的数列的所有项之和记为 $\text{[math]}$ ．
1. （1）设第 $\text{[math]}$ 次构造后得的数列为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ，请用含 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的代数式表达出 $\text{[math]}$ ，并推导出 $\text{[math]}$ 与 $\text{[math]}$ 满足的关系式；
2. （2）求数列 $\text{[math]}$ 的通项公式 $\text{[math]}$ ；
3. （3）证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024高二下·宝安月考) 已知函数 $\text{[math]}$ ．
1. （1）讨论 $\text{[math]}$ 的单调性．
2. （2）证明：当 $\text{[math]}$ 时， $\text{[math]}$ ．
3. （3）证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题