湖北省黄冈市麻城市2023-2024学年九年级下学期数学期中...

更新时间：2024-06-27 浏览次数：5 类型：期中考试

一、选择题：(共10题，每题3分，共30分．在每小题给出的选项中，只有一项符合

1. 在1， 0， $\text{[math]}$ ， $\text{[math]}$ 这四个数中，最小的数是（）

A . 1 B . 0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列图形，是轴对称图形但不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·商丘模拟) 把不等式组 $\text{[math]}$ 的解集表示在数轴上，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 下列说法正确的是（）

A . 可能性是99%的事件在一次实验中一定会发生 B . 了解全国中学生视力情况，采用全面调查的方式 C . 了解举水河的水质情况，采用抽样调查的方式 D . 从 2000 名学生中随机抽取 100 名学生进行调查，样本容量为 2000

答案解析收藏纠错 + 选题
6. (2020七下·江阴月考) 把一块直尺与一块含30°的直角三角板如图放置，若∠1＝34°，则∠2的度数为（）

A . 114° B . 124° C . 116° D . 126°

答案解析收藏纠错 + 选题
7. (2017·官渡模拟) 一个正多边形的内角和为1080°，则这个正多边形的每个外角为（）

A . 30° B . 45° C . 60° D . 80°

答案解析收藏纠错 + 选题
8. 我们知道，四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形 $\text{[math]}$ 的边 $\text{[math]}$ 在x轴上， $\text{[math]}$ 的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点 $\text{[math]}$ 处，则点C的对应点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 如图PA、PB是圆O的切线，切点分别为A、B，点C在AB上，过C作圆O的切线分别交PA、PB于点D、E，连接OD、OE，若∠P=50°，则∠DOE的度数为（　　　）

A . 130° B . 50° C . 60° D . 65°

答案解析收藏纠错 + 选题
10. 在平面直角坐标系xOy中，O为坐标原点，抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ 与x轴的一个交点位于 $\text{[math]}$ ， $\text{[math]}$ 两点之间．下列结论：其中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 若 $\text{[math]}$ 、 $\text{[math]}$ 为方程 $\text{[math]}$ 的两个根，则 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题： (共5题， 每题3分， 共 15分)

11. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. 已知某一次函数的图象经过点 $\text{[math]}$ ，且函数y的值随自变量x的增大而减小，请写出一个符合上述条件的函数关系式：．

答案解析收藏纠错 + 选题
13. “二十四节气”是上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”．若要从“二十四节气”主题邮票中的“立春”“芒种”“秋分”“大寒”四张邮票中随机抽取两张，则恰好抽到“芒种”和“秋分”两张邮票的概率是．

答案解析收藏纠错 + 选题
14. 桔槔俗称“吊杆”“称杆”（如图1），是我国古代农用工具，是一种利用杠杆原理的取水机械，桔槔示意图如图2所示， $\text{[math]}$ 是垂直于水平地面的支撑杆， $\text{[math]}$ 米， $\text{[math]}$ 是杠杆， $\text{[math]}$ 米， $\text{[math]}$ ，当点A位于最高点时， $\text{[math]}$ ，此时，点A到地面的距离为．

答案解析收藏纠错 + 选题
15. 将矩形 $\text{[math]}$ 的边 $\text{[math]}$ 向 $\text{[math]}$ 折叠，使点B恰好落在边 $\text{[math]}$ 上，记为点 $\text{[math]}$ ，将边 $\text{[math]}$ 向着 $\text{[math]}$ 折叠，使点D恰好落在 $\text{[math]}$ 上，记为点 $\text{[math]}$ ．两次折痕分别为 $\text{[math]}$ ，若 $\text{[math]}$ ，两次落点的距离 $\text{[math]}$ ，则矩形 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题

三、解答题：(本题共9小题，共 75分．解答应写出文字说明，证明过程或演算步骤)

16. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021九上·秦都月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点E，延长 $\text{[math]}$ 至F点，使 $\text{[math]}$ ，连接 $\text{[math]}$ .求证：四边形 $\text{[math]}$ 是矩形.

答案解析收藏纠错 + 选题
18. (2018·长春模拟) 在大城市，很多上班族选择“低碳出行”，电动车和共享单车成为他们的代步工具．某人去距离家8千米的单位上班，骑共享单车虽然比骑电动车多用20分钟，但却能强身健体，已知他骑电动车的速度是骑共享单车的1.5倍，求骑共享单车从家到单位上班花费的时间．

答案解析收藏纠错 + 选题
19. 为了了解中学生对党史知识知晓情况，某校开展了以“不忘初心，牢记使命”为主题的知识竞赛，现从该校八、九年级各随机抽取10名学生的成绩进行整理，描述和分析(成绩用m表示)，共分成四个组：A ． $\text{[math]}$ ， B． $\text{[math]}$ ， C ． $\text{[math]}$ ， D． $\text{[math]}$ ．另外给出了部分信息如下：
八年级10名学生的成绩： 99， 80， 99， 86， 99， 96， 90， 100， 89， 82．
九年级 10 名学生的成绩在C组的数据： 94， 90， 94．
八、九年级抽取学生成绩统计表
年级
八年级
九年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
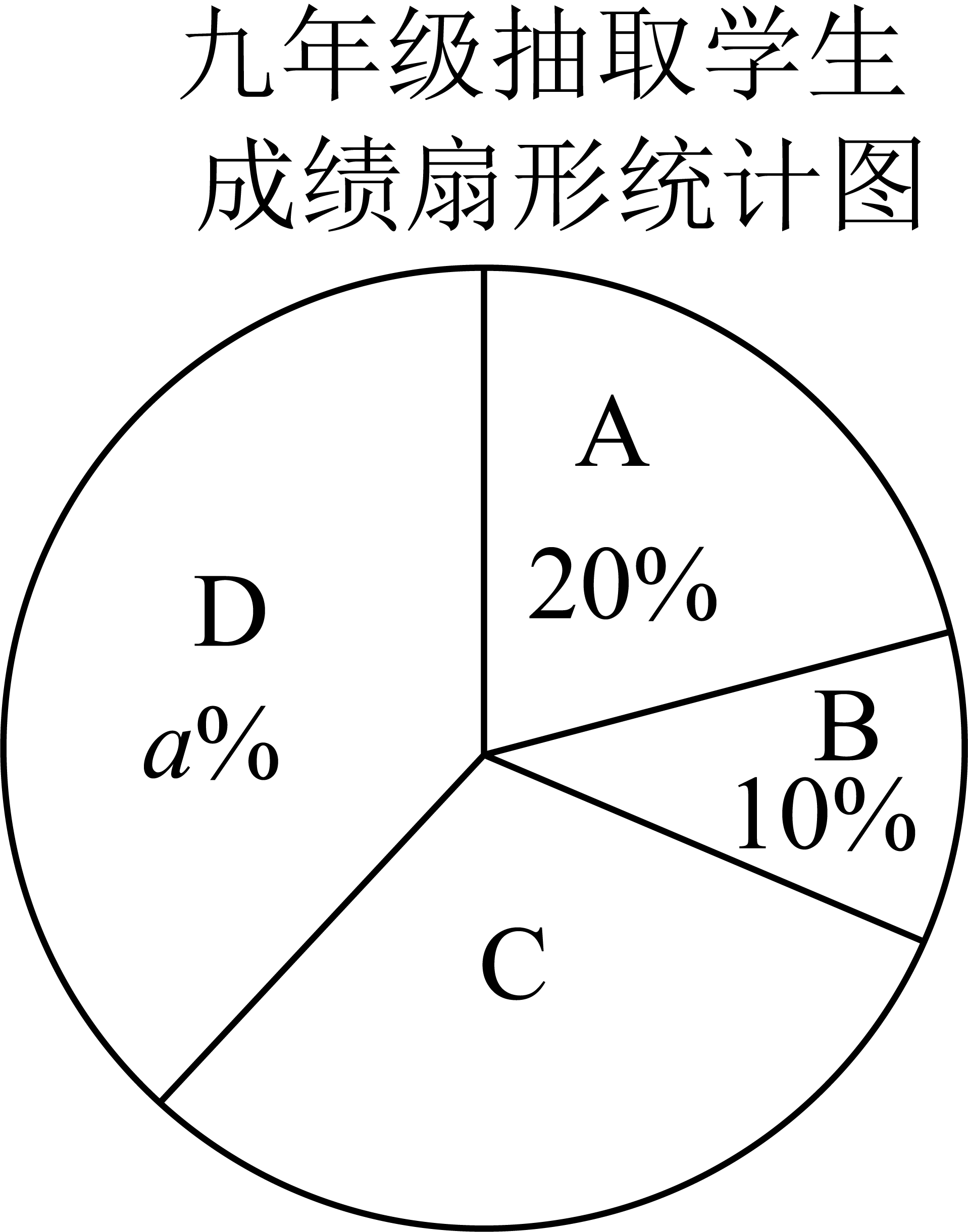
根据以上信息，解答下列问题：
1. （1）上面图表中的 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．扇形统计图中“D组”所对应的圆心角的度数为．
2. （2）该校九年级共有840 名学生参加了知识竞赛活动，估计九年级参加此次知识竞赛活动成绩为较好 $\text{[math]}$ 的学生有多少人?
3. （3）根据以上信息，你认为哪个年级的学生对“不忘初心，牢记使命”的内容掌握较好? 说明理由． (一条即可)
答案解析收藏纠错 + 选题
20. (2023·贵州) 如图，在平面直角坐标系中，四边形 $\text{[math]}$ 是矩形，反比例函数 $\text{[math]}$ 的图象分别与 $\text{[math]}$ 交于点 $\text{[math]}$ 和点 $\text{[math]}$ ，且点 $\text{[math]}$ 为 $\text{[math]}$ 的中点．
1. （1）求反比例函数的表达式和点 $\text{[math]}$ 的坐标；
2. （2）若一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，当点 $\text{[math]}$ 在反比例函数图象上 $\text{[math]}$ 之间的部分时（点 $\text{[math]}$ 可与点 $\text{[math]}$ 重合），直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
21. 如图 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 过点 $\text{[math]}$ ，分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于 $\text{[math]}$ 、 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线：
2. （2）若 $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分面积．
答案解析收藏纠错 + 选题
22. 某款旅游纪念品很受游客喜爱，每个纪念品进价40元，规定销售单价不低于44元，且不高于52元．某商户在销售期间发现，当销售单价定为44元时，每天可售出300个，销售单价每上涨1元，每天销量减少10个．现商家决定提价销售，设每天销售量为y个，销售单价为x元．
1. （1）写出y与x之间的函数关系式和自变量x的取值范围；
2. （2）将纪念品的销售单价定为多少元时，商家每天销售纪念品获得的利润w元最大？最大利润是多少元？
3. （3）该商户从每天的利润中捐出200元做慈善，为了保证捐款后每天剩余利润不低于2200元，求销售单价x的范围．
答案解析收藏纠错 + 选题
23. 某校数学活动小组探究了如下数学问题：
1. （1）问题发现：如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．点P是底边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为腰作等腰 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、则 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系是；
2. （2）变式探究：如图2， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．点P是腰 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为底边作等腰 $\text{[math]}$ ，连接 $\text{[math]}$ ，判断 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由；
3. （3）问题解决：如图3，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一点，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ，点 $\text{[math]}$
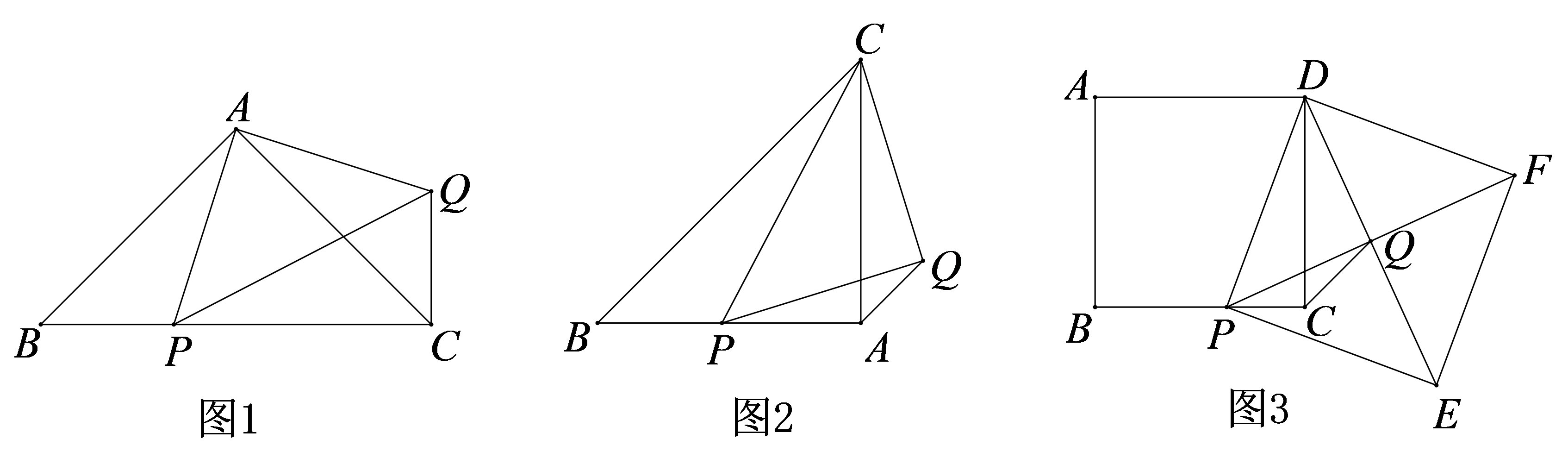
  是正方形 $\text{[math]}$ 两条对角线的交点，连接 $\text{[math]}$ ．若正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出正方形 $\text{[math]}$ 的边长．
答案解析收藏纠错 + 选题
24. 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，点D是抛物线上横坐标为6的点．点P在这条抛物线上，且不与A、D两点重合，过点P作y轴的平行线与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ，过点Q作 $\text{[math]}$ 垂直于y轴，点F在点Q的右侧，且 $\text{[math]}$ ，以 $\text{[math]}$ 、 $\text{[math]}$ 为邻边作矩形 $\text{[math]}$ ．设矩形 $\text{[math]}$ 的周长为 $\text{[math]}$ ，点 $\text{[math]}$ 的横坐标为m ．
1. （1）求这条抛物线所对应函数表达式．
2. （2）求这条抛物线的对称轴将矩形 $\text{[math]}$ 的面积分为1：2 两部分时m的值．
3. （3） ①求d与m之间的函数关系式，
  ②根据d的不同取值，试探索点P的个数情况．
答案解析收藏纠错 + 选题