一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A . 小明在荡秋千
B . 拉开抽屉
C . 行驶中的车轮滚动
D . 运动的钟摆
-
A . 点 和点
和点 B . 点
B . 点 和点
和点 C . 点
C . 点 和点
和点 D . 点
D . 点 和点
和点
-
A . 35°
B . 70°
C . 100°
D . 110°
-
A . 图中的 与
与 是同位角
B . 图中的
是同位角
B . 图中的 与
与 是同旁内角
C . 图中的
是同旁内角
C . 图中的 与
与 是邻补角
D . 图中的
是邻补角
D . 图中的 与
与 是对顶角
是对顶角
-
A . 平行
B . 相交但不垂直
C . 垂直
D . 无法确定
-
A . 45°
B . 35°
C . 30°
D . 25°
-
7.
(2024七下·威县月考)
在同一平面内,小明将一到三角板按如图所示的位置摆放,可以画出线段

和线段

, 且

, 在不添加辅助线的情况下,

的依据是( )

A . 两直线平行,同位角相等
B . 同位角相等,两直线平行
C . 两直线平行,内错角相等
D . 内错角相等,两直线平行
-
8.
(2024七下·威县月考)
在同一平面内,直线

外有一点

, 直线

上有

,

,

三点.若

,

,

, 则点

到直线

的距离
可能为( )
-
9.
(2024七下·威县月考)
如图,施工以从点

出发,沿北偏东62°方向修公路

, 在

段出现塌陷区,后改变方向,由点

沿北偏西38°的方向继续修建

段,到达点

又改变方向,从点

继续修建

段,若要使路段

, 则

的度数应为( )

A . 110°
B . 100°
C . 90°
D . 80°
-
10.
(2024七下·威县月考)
如图,在三角形

中,点

,

,

分别在

,

,

上,且

,

,

, 则图中
一定与

(除

外)相等的角有( )

A . 2个
B . 3个
C . 4个
D . 5个
-
11.
(2024七下·威县月考)
一次数学活动中,检验两条纸带①、②的边线是否平行,嘉嘉和淇淇采用两种不同的方法:嘉嘉将纸带①沿

折叠,量得

;淇淇将纸带②沿

折叠,发现

与

重合,

与

重合(点

在

上,点

在

上),如图所示.下列判断正确的是( )

A . 只有纸带①的边线平行
B . 只有纸带②的边线平行
C . 纸带①、②的边线都平行
D . 纸带①、②的边线都不平行
-
12.
(2024七下·威县月考)
如图,

,

,

, 垂足为

,

平分

. 关于结论Ⅰ、Ⅱ,下列判断正确的是( )

结论Ⅰ: ;
;
结论Ⅱ:若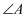 (
( )的度数每增加2°,则
)的度数每增加2°,则 的度数会减少1°
的度数会减少1°
A . 结论Ⅰ、Ⅱ都正确
B . 结论Ⅰ、Ⅱ都不正确
C . 只有结论Ⅰ正确
D . 只有结论I正确
二、填空题(本大题共4个小题,每小题3分,共12分)
-
-
-
15.
(2024七下·威县月考)
如图,为美化校园,某校要在长12米,宽6米的长方形空地中划出三个小长方形(阴影部分),若小长方形的宽均为2米,则空白部分的面积为
平方米.

-
16.
(2024七下·威县月考)
如图,把一块三角放

(

)90°角的顶点

放在长方形

的边

上,保持点

的位置不动,在转动三角板

时,若

与长方形

的边平行,则

的度数为
.

三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤).
-
-
(1)
将三角形

向右平移4个单位长度,再向上平移1个单位长度后,得到三角形

, 点

,

,

的对应点分别是点

,

,

, 请在图中画出平移后的三角形

;
-
(2)
在(1)的基础上,连接

,

.
① 与
与 之回的数量关系为;
之回的数量关系为;
②四边形 的面积为.
的面积为.
-
-
(1)
从汽车站

到码头

怎样走最近?画出最近路线,并说明理由;
-
(2)
从码头

到公路

怎样走最近?画出最近路线

, 并说明理由;
-
(3)
在(1),(2)的基础上,比较

和

的大小.
-
-
(1)
判断

与

之间的位置关系,并说明理由;
-
(2)
若

, 求证

.
-
-
(1)
写出该命题的题设和结论,并将其改写成“如果……那么……”的形式;
-
-
-
-
(2)
若

平分

,

,

, 求

的度数(用舍

的式子表示).
-
-
(1)
分别求

和

的度数;
-
(2)
若

,

, 求图中阴影部分的面积;
-
(3)
已知点

在三角形

约内部,三角形

平移到三角形

后,点

的对应点为

, 连接

. 若三角形

的周长为

, 四边形

的周长为

, 请
直接写出

的长度.
-
-
(1)
若

,

, 求光的传播方向改变了多少度;
-
(2)
请判断射入光线

与射出光线

是否平行,并说明理由;
-
(3)
已知光线

与

的夹角为35°,如图3所示.若射出光线

与光线

垂直,则

的度数为
.
-
24.
(2024七下·威县月考)
如图1、图2,直线

,

被射线

所截,且

,

是射线

上的定点,点

在射线

上,连接

, 过点

作

, 与直线

交于点

, 且

.

-
-
(2)
若点

在线段

上(点

不与点

,

重合).
①依题意,在图2中补全图形;
②猜想 与
与 之间的数量关系,并证明;
之间的数量关系,并证明;
-




与
之回的数量关系为;
的面积为.
, 直线
截
,
于点
,
.

.
(已知),
().
(平角的定义),
().
斜射到一块玻璃砖的上表面
上的点
处,并在下表面
(
)的点
处射出,
于点
, 如图2所示,图中所有的点都在同一平面内,查问相关科学知识,得到
.

与
之间的数量关系,并证明;