吉林省长春市朝阳区长春北湖学校2024年中考一模数学模拟试题

更新时间：2024-07-11 浏览次数：71 类型：中考模拟

一、选择题（本大题共8小题，每小题3分，共24分）

1. (2024·朝阳模拟) 在实数－3，0， $\text{[math]}$ ， 1.8中，最小的是（）

A . －3 B . 0 C . $\text{[math]}$ D . 1.8

答案解析收藏纠错 + 选题
2. (2024·朝阳模拟) 下列计算正确的是（）

A . a^3.a²＝a⁶ B . a³＋a²＝2a⁵ C . （3a³）²＝9a⁶ D . a⁸÷a²＝a⁴

答案解析收藏纠错 + 选题
3. (2024·朝阳模拟) 一元一次不等式组 $\text{[math]}$ 的解集为（）

A . x＜1 B . x＜4 C . 1＜x＜4 D . 无解

答案解析收藏纠错 + 选题
4. (2024·朝阳模拟) 如图是正方体展开图，将 $\text{[math]}$ 论语 $\text{[math]}$ 十二章中的一句话：“学而不思则罔”这六个字写在正方体展开图的六个面内，则“而”对面的文字是（）

A . 不
B . 思
C . 则
D . 罔

答案解析收藏纠错 + 选题
5. (2024·朝阳模拟) 如图，△ABC中BC边上的高为 $\text{[math]}$ ， △DEF中DE边上的高为 $\text{[math]}$ ，若AC＝EF ，则下列关于 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系的说法正确的是（）

A . $\text{[math]}$ ＜ $\text{[math]}$ B . $\text{[math]}$ ＝ $\text{[math]}$ C . $\text{[math]}$ ＞ $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
6. (2024·朝阳模拟) 如图，在坡比为i＝1∶2.5的山坡种树，要求株距（相邻两棵树之间的水平距离）为5m，那么相邻两棵树间的坡面距离为（）

A . 2.5m B . 5m C . 6.25m D . $\text{[math]}$ m

答案解析收藏纠错 + 选题
7. (2024·朝阳模拟) 如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：
①作线段AB ，分别以A ， B为圆心，以AB长为半径作弧，两弧的交点为C；
②以点C为圆心，仍以AB长为半径作弧交AC的延长线于点D；
③连结BD、BC ．则下列说法不正确的是（）

A . △ABC是正三角形 B . ∠CBD＝30° C . 点C在BD的中垂线上 D . cosD＝ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·朝阳模拟) 如图，在平面直角坐标系中，点A、B在第一象限，且AB⊥x轴，点P为线段AB的中点，函数y＝ $\text{[math]}$ 、y＝ $\text{[math]}$ 、y＝ $\text{[math]}$ 的图象分别经过点A、P、B ，若 $\text{[math]}$ ＝2，则 $\text{[math]}$ 的值为（）

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

9. (2024·富阳模拟) 因式分解：x²-4=

答案解析收藏纠错 + 选题
10. (2024·朝阳模拟) 一件商品的进价是a元，提价30%后出售，则这件商品的售价是元．

答案解析收藏纠错 + 选题
11. (2024·朝阳模拟) 关于x的一元二次方程x²－3x＋m＝0有两个不相等的实数根，则正整数m的值可以是．（写出一个符合题意的值即可）

答案解析收藏纠错 + 选题
12. (2024·朝阳模拟) 图中的交通禁令标志是停车让行标志，此标志形状为各角均相等的八角形，在中间加停字，红底白字白边，表示车辆必须在停止线以外停车瞭望，确认安全后，才准许通行，该标志中八角形的一个内角是度．

答案解析收藏纠错 + 选题
13. (2024·朝阳模拟) 如图，已知△ABC与△DEF位似，位似中心为点O ．若 $\text{[math]}$ ， △ABC的周长与△DEF的周长之比为．

答案解析收藏纠错 + 选题
14. (2024·朝阳模拟) 对于二次函数y＝ax²＋bx＋c（a≠0，a为整数），有四种说法：①函数与x轴的一个交点为（－1，0）；②对称轴为直线x＝1；③当a＞0时，函数的最小值为3；④点（2，8）在函数图象上．若其中只有一个说法是错误的，则a的值为．

答案解析收藏纠错 + 选题

三、解答题（本大题共10小题，共78分）

15. (2024·朝阳模拟) 先化简，再求值：（x＋2）（x－3）－（x－2）² ，其中x＝－ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024·朝阳模拟) 人工智能是数字经济高质量发展的引擎，也是新一轮科技革命和产业变革的重要驱动，人工智能市场在应用领域分为决策类人工智能，人工智能机器人，语音类人工智能，视觉类人工智能四大类型，将四个类型的图标依次制成A ， B ， C ， D四张卡片（卡片背面完全相同）将四张卡片背面朝上洗匀放置在桌面上从中随机抽取一张，记录卡片的内容质放回洗匀，再随机抽取一张，请用列表或画树状图的方法求抽取到的两张卡片内容一致的概率．

答案解析收藏纠错 + 选题
17. (2024·朝阳模拟) 如图，在四边形ABCD中，AB//CD ，点E在边AD上，且 DE＝DC ，连结CE ．当CE平分∠BCD时，求证：AB＝CD ．

答案解析收藏纠错 + 选题
18. (2024·朝阳模拟) 为了大力弘扬中华优秀传统文化，某校决定开展名著读书活动，用3600元购买“四大名著”若干套后，发现这批图书满足不了学生的阅读需求，图书管理员在购买第二批时正赶上图书城8折销售该套书，于是用2400元购买的套数只比第一批少4套，求第一批购进的“四大名著”每套的价格是多少元．

答案解析收藏纠错 + 选题
19. (2024·朝阳模拟) 图①、图②、图③均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，每个小正方形的边称为格线，点A、点B、点C均在格点上，点P、点M在格线上，只用无刻度的直尺，在给定的正方形网格中，分别按下列要求画图，保留作图痕迹．
1. （1）在图①中，画CD∥AB ，且点D在格点上；
2. （2）在图②中，先标记PC的中点O ，再画点B关于点O的对称点E；
3. （3）在图③中，以点A、B、M为顶点画平行四边形ABMN ．
答案解析收藏纠错 + 选题
20. (2024·朝阳模拟) 青少年体重指数（BMI）是评价青少年营养状况、肥胖的一种衡量方式，体重指数BM I计算公式为： $\text{[math]}$ ，其中G表示体重（kg），h表示身高（m）．《国家学生体质健康标准》将学生体重指数（BMI）分成四个等级，如下表：
等级
偏瘦（A）
标准（B）
超重（C）
肥胖（D）
男
BMI≤15.7
15.7＜BMI≤22.5
22.5＜BMI≤25.4
BMI＞25.4
女
BMI≤15.4
15.4＜BMI≤22.2
22.2＜BMI≤24.8
BMI＞24.8
为了解学校学生体重指数分布情况，数学综合实践小组开展了一次调查．
【数据收集】小组成员从本校学生中随机抽取部分学生进行问卷调查，并收集数据；
【数据整理】调查小组根据收集的数据，绘制了两组不完整的统计图．
【问题解决】根据以上信息，解决下列问题：
1. （1）若一位男生的身高为1.6m，体重为51.2kg，则他的体重指数（BMI）属于等级；（填“A”，“B”，“C”，“D"）
2. （2）求本次调查的总人数，并补全条形统计图；
3. （3）求扇形统计图中表示体重指数（BMI）“A”等级的扇形的圆心角的度数；
4. （4）若该校共有男学生1200名，女学生1100名，估计全校体重指数为“肥胖”的学生约为多少人？
答案解析收藏纠错 + 选题
21. (2024·朝阳模拟) 某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯，小李和妈妈两人从二楼同时下行，妈妈乘自动扶梯，小李走步行楼梯，妈妈离一楼地面的高度h（单位：m）与下行时间x（单位：s）之间满足一次函数关系，其部分对应数据如表所示，小李离一楼地面的高度y（单位．m）与下行时间x（单位：s）的函数关系如图所示．
x
…
1
3
5
…
h
…
5.4
4.2
3
…
1. （1）求y与x的函数表达式；
2. （2）请通过计算说明小李和妈妈两人谁先到达一楼地面．
答案解析收藏纠错 + 选题
22. (2024·朝阳模拟) 在等边△ABC中，AB＝4，以A为圆心，2为半径画60°的DE ．
1. （1）【特例感知】如图①，当点D、E分别在AB、AC上时，BD与CE的数量关系为．（不需要证明）
2. （2）【一般探究】如图②，将图①中的扇形EAD绕点A转动，在旋转过程中，上述（1）的数量关系还存在吗？请说明理由．
3. （3）【思维拓展】如图②，在扇形EAD旋转过程中，当点B、E、D三点共线时，CE的长为．
答案解析收藏纠错 + 选题
23. (2024·朝阳模拟) 如图，在正方形ABCD中，动点P从点A出发，沿A－B－C运动到点C停止．过点C作DP的垂线，垂足为点G ，延长CG到点E ，使EG＝CG ，连结DE ， AE ，直线EA与DP交于点F ．设∠ADP为 $\text{[math]}$ ，且0°＜ $\text{[math]}$ ＜90°．
1. （1）当 $\text{[math]}$ ＝10°时，∠ADE＝°，∠DAE＝°；
2. （2）当点P在AB上时，
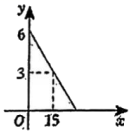
  ①求sinF的值；
  ②当△DEF为轴对称图形时，求 $\text{[math]}$ 的大小；
3. （3）若正方形ABCD的面积为4，直接写出△DAF面积的最大值．
答案解析收藏纠错 + 选题
24. (2024·朝阳模拟) 在平面直角坐标系中抛物线y＝ax²＋bx＋3交x轴于点A（－1，0）、B（3，0），交y轴于点C ，连结AC、BC ．点D在该抛物线上，过点D作DE//AC ，交直线BC于点E ，连结AD、AE、BD ．设点D横坐标为m（m＞0），△DAE的面积为 $\text{[math]}$ ， △DBE的面积为 $\text{[math]}$ ．
1. （1）求a ， b的值；
2. （2）设抛物线上D、B两个点和它们之间的部分为图象G ，当图象G的最高点的纵坐标与m无关时，求m的取值范围；
3. （3）当点D在第一象限时，求 $\text{[math]}$ ＋ $\text{[math]}$ 的最大值；
4. （4）当 $\text{[math]}$ ∶ $\text{[math]}$ ＝2∶1时，直接写出m的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

吉林省长春市朝阳区长春北湖学校2024年中考一模数学模拟试题

副标题：

*注意事项：

吉林省长春市朝阳区长春北湖学校2024年中考一模数学模拟试题

试题分析

总体分析

题量分析

难度分析

知识点分析

等级	偏瘦（A）	标准（B）	超重（C）	肥胖（D）
男	BMI≤15.7	15.7＜BMI≤22.5	22.5＜BMI≤25.4	BMI＞25.4
女	BMI≤15.4	15.4＜BMI≤22.2	22.2＜BMI≤24.8	BMI＞24.8

x	…	1	3	5	…
h	…	5.4	4.2	3	…