北京市第五十七中学2023-2024学年八年级下学期数学期中...

更新时间：2024-05-08 浏览次数：13 类型：期中考试

一、选择题（本题共 20 分，每小题 2 分）

1. 下列各组数据能组成直角三角形的是（）

A . 2，3，4 B . 4，5，6 C . 8，15，17 D . 11，12，13

答案解析收藏纠错 + 选题
2. (2023八下·右玉期末) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点O，且 $\text{[math]}$ ， $\text{[math]}$ ．则 $\text{[math]}$ 的周长为（）

A . 13 B . 8 C . 7 D . 5

答案解析收藏纠错 + 选题
3. 下列等式不成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 图1是一面旗帜，图2是其示意图，四边形 $\text{[math]}$ 是平行四边形，点 E 在线段 $\text{[math]}$ 的延长线上，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 如图，在水塔 O 的东北方向 $\text{[math]}$ 处有一抽水站 A ，在水塔的东南方向 $\text{[math]}$ 处有一建筑工地B ，在 $\text{[math]}$ 间建一条直水管，则水管的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八下·睢县期末) 如图，在四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，OB=OD，下列结论不一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 在 $\text{[math]}$ 中， D 为斜边 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是（）

A . 5 B . 3 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. 如图，四边形 $\text{[math]}$ 和四边形 $\text{[math]}$ 都是矩形，且点A在 $\text{[math]}$ 上，设矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 的面积分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
9. 图，正方形ABCD的面积为4，菱形AECF的面积为2，则EF的长是（　　）

A . 1 B . $\text{[math]}$ C . 2 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
10. 如图，点E在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上，将 $\text{[math]}$ 绕点A顺时针旋转 $\text{[math]}$ 到 $\text{[math]}$ 的位置，连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ 的垂线，垂足为点H ，与 $\text{[math]}$ 交于点G ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 8 D . 9

答案解析收藏纠错 + 选题

二、填空题（本题共 16 分，每小题 2 分）

11. 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 度数为．

答案解析收藏纠错 + 选题
12. (2019·永州) 使代数式 $\text{[math]}$ 有意义的x的取值范围是．

答案解析收藏纠错 + 选题
13. 已知 $\text{[math]}$ ，化简 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. 如图，在数轴上点A表示的实数是．

答案解析收藏纠错 + 选题
15. 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 的顶点D在x轴上，边 $\text{[math]}$ 在y轴上，若点A的坐标为 $\text{[math]}$ ，则点B的坐标为．

答案解析收藏纠错 + 选题
16. 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 对折至 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 刚好是 $\text{[math]}$ 边的中点，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
17. (2022八下·蜀山期末) 如图，菱形ABCD的对角线AC， BD相交于点O，P为AB边上一动点（不与点A，B重合），PE⊥OA于点E，PF⊥OB于点F，若AB=8，∠BAD=60°，则线段EF长度的最小值为．

答案解析收藏纠错 + 选题
18. 如图，点 A ， B ， C 为平面内不在同一直线上的三点．点 D 为平面内一个动点．线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中点分别为 M ， N ， P ， Q 在点 D 的运动过程中，有下列结论：
①存在无数个中点四边形 $\text{[math]}$ 平行四边形；
②只有有限个中点四边形 $\text{[math]}$ 是菱形；
③存在无数个中点四边形 $\text{[math]}$ 矩形；
④存在两个中点四边形 $\text{[math]}$ 正方形．
所有正确结论的序号是．

答案解析收藏纠错 + 选题

三、解 答 题（本题共 64分，第 19、28每 题 8分，第 20、21、22每题 5分，第 23、24每题 6 分，第 25-27题每题7分）

19. 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. 下面是“作三角形一边中线”的尺规作图过程
已知： $\text{[math]}$
求作： $\text{[math]}$ 边上的中线 $\text{[math]}$ ．
作法：如图，
①分别以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径作弧，两弧相交于 $\text{[math]}$ 点；
②作直线 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ 点，所以线段 $\text{[math]}$ 就是所求作的中线．
根据上述的作法，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明
  证明： ∵ $\text{[math]}$
  ∴四边形 $\text{[math]}$ 是平行四边形（①）
  ∵ $\text{[math]}$ 与 $\text{[math]}$ 交于 $\text{[math]}$ 点
  ∴ $\text{[math]}$ （②）
  ∴ $\text{[math]}$ 是 $\text{[math]}$ 的中线．
答案解析收藏纠错 + 选题
21. (2022八下·斗门期末) 如图，点E，F分别是▱ABCD的边AB，CD上的一点，连接DE，BF，若∠1＝∠2，求证：四边形是DEBF是平行四边形．

答案解析收藏纠错 + 选题
22. 如图，在△ABC中，点D ，点E分别是边AC ， AB的中点，点F在线段DE上，AF＝5，BF＝12，AB＝13，BC＝19，求DF的长度．

答案解析收藏纠错 + 选题
23. 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点E ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点F ， $\text{[math]}$ 与 $\text{[math]}$ 交于点P ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. 阅读下面材料：
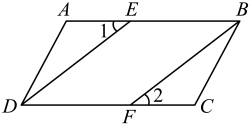
小明遇到这样一个问题：如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于D、E ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试求 $\text{[math]}$ 的值．
小明发现，过点E作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点F ，构造 $\text{[math]}$ ，经过推理得到 $\text{[math]}$ ，再计算就能够使问题得到解决（如图②）．
1. （1）请你帮小明回答： $\text{[math]}$ 的值为．
2. （2）参考小明思考问题的方法，请你解决如下问题：
  如图③，已知 $\text{[math]}$ 和矩形 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点G ， $\text{[math]}$ ，求 $\text{[math]}$ 度数．
答案解析收藏纠错 + 选题
25. 在二次根式的计算和比较大小中，有时候用“平方法”会取得很好的效果，例如，比较 $\text{[math]}$ 和 $\text{[math]}$ 的大小，我们可以把 a 和 b 分别平方， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， ∴ $\text{[math]}$
请利用“平方法”解决下面问题：
1. （1）比较 $\text{[math]}$ ， $\text{[math]}$ 大小，c d（填写 $\text{[math]}$ ， $\text{[math]}$ 或者 $\text{[math]}$ ）．
2. （2）猜想 $\text{[math]}$ ， $\text{[math]}$ 之间的大小，并证明．
3. （3）已知 $\text{[math]}$ ，化简 $\text{[math]}$ = （直接写出答案）．
答案解析收藏纠错 + 选题
26. 定义：平面内一点 $\text{[math]}$ 到点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ 三个点的距离分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，若有 $\text{[math]}$ ，则称点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点关于点 $\text{[math]}$ 的勾股点．
1. （1）若点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点关于点 $\text{[math]}$ 的勾股点，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）如图1， $\text{[math]}$ 与 $\text{[math]}$ 都是等腰直角三角形， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为边 $\text{[math]}$ 上一动点．求证：点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点关于点 $\text{[math]}$ 的勾股点；
3. （3）如图2， $\text{[math]}$ 为直角三角形， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点关于点 $\text{[math]}$ 的勾股点，连接 $\text{[math]}$ ， $\text{[math]}$ ，作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为．
答案解析收藏纠错 + 选题
27. 在 $\text{[math]}$ 中， $\text{[math]}$ ， E是线段 $\text{[math]}$ 上一动点，连接 $\text{[math]}$ ．
1. （1）如图1，若 $\text{[math]}$ ， $\text{[math]}$ 的面积为；
2. （2）如图2，若 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕C ，逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ．若点G是线段 $\text{[math]}$ 的中点，过点G作 $\text{[math]}$ 交 $\text{[math]}$ 于点P ，交 $\text{[math]}$ 于点H ，证明 $\text{[math]}$ ；
3. （3）如图3，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折至 $\text{[math]}$ ，连接 $\text{[math]}$ ． D是线段 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，直接写出当 $\text{[math]}$ 取得最小值时的长度．
答案解析收藏纠错 + 选题
28. 在平面直角坐标系 $\text{[math]}$ 中，对于没有公共点的两个图形M、N给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，若P、Q两点间距离的最大值和最小值分别为 $\text{[math]}$ 和 $\text{[math]}$ ，则称比值 $\text{[math]}$ 为图形M和图形N的“友谊关联值”，记为 $\text{[math]}$ ．已知 $\text{[math]}$ 顶点坐标为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若E为 $\text{[math]}$ 边上任意一点，则 $\text{[math]}$ 的最大值为，最小值为，因此 $\text{[math]}$ （点O ， $\text{[math]}$ ） $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ 为 $\text{[math]}$ 对角线 $\text{[math]}$ 上一点， $\text{[math]}$ 为 $\text{[math]}$ 对角线 $\text{[math]}$ 上一点，其中 $\text{[math]}$ ．
  ①若 $\text{[math]}$ ，则 $\text{[math]}$ （线段 $\text{[math]}$ ， $\text{[math]}$ ） $\text{[math]}$ ；
  ②若 $\text{[math]}$ （线段 $\text{[math]}$ ， $\text{[math]}$ ） $\text{[math]}$ ，求m的取值范围；
3. （3）若 $\text{[math]}$ 的对角线交点为O ，且顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，其中 $\text{[math]}$ ，请直接用含n的代数式表示 $\text{[math]}$ ．．
答案解析收藏纠错 + 选题