一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
2.
(2024·临沂一模)
某商城开设一种摸奖游戏,中一等奖的机会为20万分之一,将这个数用科学记数法表示为( )
A . 2×10﹣5
B . 2×10﹣6
C . 5×10﹣5
D . 5×10﹣6
-
-
-
-
6.
(2024八下·章丘月考)
世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输

兆数据,依题意,可列方程是( )
-
7.
(2024·临沂一模)
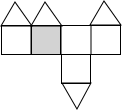
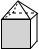
如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
-
8.
(2024·临沂一模)
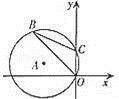
如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
-
9.
(2024·临沂一模)
如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到

. 若反比例函数

的图象恰好经过

的中点D,则k的值是( )

A . 9
B . 12
C . 15
D . 18
-
10.
(2024·临沂一模)
抛物线

上的部分点的横坐标

与纵坐标

的对应值如下表:则下列结论:①

;②

;③抛物线的对称轴为直线

;④方程

的两个根为

,

. 正确的有( )
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
13.
(2024·临沂一模)
为了落实“双减”政策,东营市某学校对初中学生

课外作业时长进行了问卷调查,15名同学的作业时长统计如下表,则这组数据的众数是
分钟.
作业时长(单位:分钟) | 50 | 60 | 70 | 80 | 90 |
人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
-
-
-
16.
(2024·临沂一模)
如图,

是等腰直角三角形,直角顶点与坐标原点重合,若点
B在反比例函数


图象上,则经过点
A的反比例函数表达式为
.

三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
-
18.
(2024·临沂一模)
6月5日是世界环境日.某校举行了环保知识竞赛,从全校学生中随机抽取了n名学生的成绩进行分析,并依据分析结果绘制了不完整的统计表和统计图(如下图所示).
学生成绩分布统计表
成绩/分 | 组中值 | 频率 |
75.5≤x<80.5 | 78 | 0.05 |
80.5≤x<85.5 | 83 | a |
85.5≤x<90.5 | 88 | 0.375 |
90.5≤x<95.5 | 93 | 0.275 |
95.5≤x<100.5 | 98 | 0.05 |
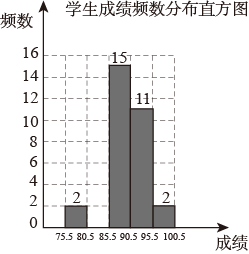
请根据以上图表信息,解答下列问题:
-
-
-
-
(4)
从成绩在75.5≤x<80.5和95.5≤x<100.5的学生中任选两名学生.请用列表法或画树状图的方法,求选取的学生成绩在75.5≤x<80.5和95.5≤x<100.5中各一名的概率.
-
19.
(2024·临沂一模)
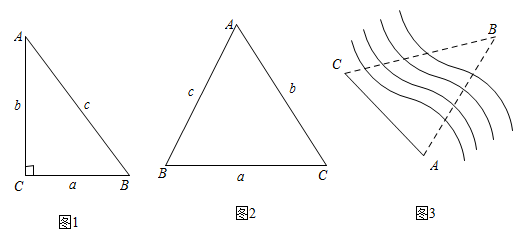
知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵ ,
, 
∴ ,
, 
∴
-
(1)
拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究

,

,

之间的关系,并写出探究过程.
-
(2)
解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
-
20.
(2024·临沂一模)
开学初,小芳和小亮去学校商店购买学习用品,已知每支钢笔

价格比每本笔记本的价格少

元,小芳用

元钱购买钢笔的数量是小亮用

元钱购买笔记本数量的

倍.
-
-
(2)
一模后,班主任再次购买上述价格的钢笔和笔记本共

件作为奖品,奖励给一模中表现突出和进步的同学,总费用不超过

元.请问至少要买多少支钢笔?
-
21.
(2024·临沂一模)
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过D作EF⊥AC于点E,交AB的延长线于点F.

-
-
(2)
当∠BAC=60°,AB=8时,求EG的长;
-
-
22.
(2024·临沂一模)
如图,直线
AC与函数
y=﹣

的图象相交于点
A(﹣1,
m),与
x轴交于点
C(5,0).

-
-
(2)
直线AE在直线AC的上方,满足∠CAE=∠CAO , 求直线AE的解析式;
-
(3)
若
D是线段
AC上一点将
OD绕点
O逆时针旋转90°得到
OD',点
D'恰好落在函数
y=﹣

的图象上,求点
D的坐标.
-
23.
(2024·临沂一模)

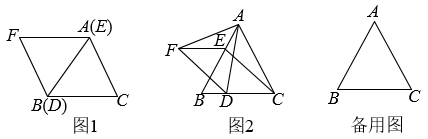
和

均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿

运动,运动到点B、C停止.
-
(1)
如图1,当点E、D分别与点A、B重合时,请判断:线段

的数量关系是
,位置关系是
;
-
(2)
如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;
-
(3)
当点D运动到什么位置时,四边形

的面积是

面积的一半,请直接写出答案;此时,四边形

是哪种特殊四边形?请在备用图中画出图形并给予证明.
-
24.
(2024·临沂一模)
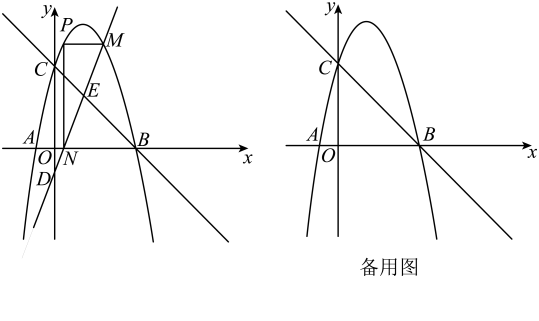
如图,直线

交

轴于点

, 交

轴于点

, 对称轴为

的抛物线经过

两点,交

轴负半轴于点

.

为抛物线上一动点,点

的横坐标为

, 过点

作

轴的平行线交抛物线于另一点

, 作

轴的垂线

, 垂足为

, 直线

交

轴于点

.
-
-
-
(3)
若

, 设直线

交直线

于点

, 是否存在这样的

值,使

?若存在,求出此时

的值;若不存在,请说明理由.
 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 
![]()
 B .
B . 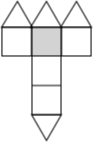 C .
C . 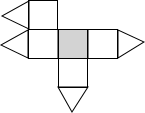 D .
D .