湖北省宜昌市第五中教联体2023-2024学年七年级下学期期...

更新时间：2024-06-14 浏览次数：15 类型：期中考试

一、选择题（共10小题）

1. (2024七下·宜昌期中) 下列值中，能满足 $\text{[math]}$ 在实数范围内有意义的是（）

A . a＝﹣2 B . a＝﹣1 C . a＝﹣0.0001 D . a＝2021

答案解析收藏纠错 + 选题
2. (2024七下·宜昌期中) 下列二次根式中，与 $\text{[math]}$ 的积是无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·当阳期末) 下列计算中，正确的是（）

A . $\text{[math]}$ ﹣ $\text{[math]}$ ＝1 B . $\text{[math]}$ ＋ $\text{[math]}$ ＝ $\text{[math]}$ C . $\text{[math]}$ × $\text{[math]}$ ＝ $\text{[math]}$ D . $\text{[math]}$ ÷ $\text{[math]}$ ＝4

答案解析收藏纠错 + 选题
4. (2024八下·商南期末) 在▱ABCD中，若∠A：∠B＝1：2，则∠A的度数为（）

A . 30° B . 60° C . 120° D . 150°

答案解析收藏纠错 + 选题
5. (2024七下·宜昌期中) 如图是一个正方形和直角三角形的组合图形，直角三角形的斜边和一条直角边的长分别为10cm，8cm，则该正方形的面积为（）

A . 6cm² B . 36cm² C . 18cm² D . 2cm²

答案解析收藏纠错 + 选题
6. (2024七下·宜昌期中) 下列命题的逆命题是假命题的是（　　）

A . 全等三角形的对应角相等 B . 两直线平行，同位角相等 C . 等边三角形三个角相等 D . 直角三角形中，斜边的平方等于两直角边的平方和

答案解析收藏纠错 + 选题
7. (2024九下·武威模拟) 如图，E为正方形ABCD的对角线上一点，四边形EFCG为矩形，若正方形ABCD的边长为4，则EG＋GC的长为（）

A . 4 B . 8 C . 16 D . 32

答案解析收藏纠错 + 选题
8. (2024七下·宜昌期中) 如图，在□ABCD中，AB＞AD ，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于 $\text{[math]}$ EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H ，则下列结论中不能由条件推理得出的是（　　）

A . AG平分∠DAB B . AD=DH C . DH=BC D . CH=DH

答案解析收藏纠错 + 选题
9. (2024七下·宜昌期中)
如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边正方形EFGH的周长为（）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . $\text{[math]}$ +1 D . 2 $\text{[math]}$ +1

答案解析收藏纠错 + 选题
10. (2024八下·宜州期中) 在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几．”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离 $\text{[math]}$ 长度为1尺．将它往前水平推送10尺时，即 $\text{[math]}$ ＝10尺，则此时秋千的踏板离地距离 $\text{[math]}$ 就和身高5尺的人一样高．若运动过程中秋千的绳索始终拉得很直，则绳索 $\text{[math]}$ 长为（）

A . 13.5尺 B . 14尺 C . 14.5尺 D . 15尺

答案解析收藏纠错 + 选题

二、填空题（共5小题）

11. (2024八下·闵行期末) 顺次连接一个矩形各边中点得到的四边形是．

答案解析收藏纠错 + 选题
12. (2024七下·宜昌期中) 将多项式 $\text{[math]}$ 在实数范围内分解因式，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024七下·宜昌期中) 已知a是负数，b是正数，化简 $\text{[math]}$ ，正确的结果是．

答案解析收藏纠错 + 选题
14. (2024七下·宜昌期中) 如图，数轴上点A对应的数为2， $\text{[math]}$ 于A ，且 $\text{[math]}$ ，以O为圆心，以 $\text{[math]}$ 为半径画圆，交数轴于点C ，则 $\text{[math]}$ 长为．

答案解析收藏纠错 + 选题
15. (2024七下·宜昌期中) 以正方形 $\text{[math]}$ 的 $\text{[math]}$ 为一边，作等边 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（共9小题）

16. (2024七下·宜昌期中) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2024七下·宜昌期中) 已知 $\text{[math]}$ ，且x ， y都是正数，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
18. (2024七下·宜昌期中) 如图，在 $\text{[math]}$ 中，点E ， F是对角线 $\text{[math]}$ 上的两点，请添加一个条件，使四边形 $\text{[math]}$ 是平行四边形，并写出证明的过程．

答案解析收藏纠错 + 选题
19. (2024七下·宜昌期中) 如图，在△ABC中，AB=13，BC=12，AC=5，点D是BC上一点，且CD=3．
1. （1）试判断△ABC的形状，并说明理由；
2. （2）求AD的长．
答案解析收藏纠错 + 选题
20. (2024八下·邕宁期中) 阅读材料，解答下列问题：
材料：已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
李聪同学是这样解答的：
∵ $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
∴ $\text{[math]}$
这种方法称为“构造对偶式”
问题：已知 $\text{[math]}$
1. （1）求 $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2024七下·宜昌期中) 研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．
1. （1）阅读材料
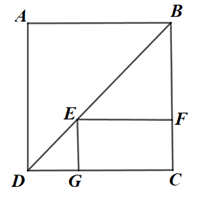
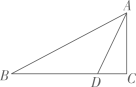
  立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．
  例如，正方体 $\text{[math]}$ （图1）．因为在平面 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点A ，所以直线 $\text{[math]}$ 与 $\text{[math]}$ 所成的 $\text{[math]}$ 就是既不相交也不平行的两条直线 $\text{[math]}$ 与 $\text{[math]}$ 所成的角．
  解决问题
  如图1，已知正方体 $\text{[math]}$ ，求既不相交也不平行的两条直线 $\text{[math]}$ 与 $\text{[math]}$ 所成角的大小．
2. （2）如图2，M ， N是正方体相邻两个面上的点．
  ①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是；
  ②在所选正确展开图中，若点M到 $\text{[math]}$ ， $\text{[math]}$ 的距离分别是2和5，点N到 $\text{[math]}$ ， $\text{[math]}$ 的距离分别是4和3，P是 $\text{[math]}$ 上一动点，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题
22. (2024七下·宜昌期中)
1. （1）阅读理解
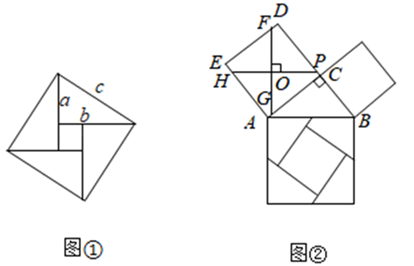
  我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程；
2. （2）问题解决
  勾股定理的证明方法有很多，如图②是古代的一种证明方法：过正方形ACDE的中心O，作FG⊥HP，将它分成4份，所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形.若AC＝12，BC＝5，求EF的值.
答案解析收藏纠错 + 选题
23. (2024七下·宜昌期中) 正方形 $\text{[math]}$ 中，点E在边 $\text{[math]}$ ， $\text{[math]}$ 上运动（不与正方形顶点重合）．作射线 $\text{[math]}$ ，将射线 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点F ．
1. （1）如图，点E在边 $\text{[math]}$ 上， $\text{[math]}$ ，则图中与线段 $\text{[math]}$ 相等的线段是；
2. （2）过点E作 $\text{[math]}$ ，垂足为G ，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
答案解析收藏纠错 + 选题
24. (2024七下·宜昌期中) 综合与实践
【问题情境】
如图1，小华将矩形纸片 $\text{[math]}$ 先沿对角线 $\text{[math]}$ 折叠，展开后再折叠，使点B落在对角线 $\text{[math]}$ 上，点B的对应点记为 $\text{[math]}$ ，折痕与边 $\text{[math]}$ ， $\text{[math]}$ 分别交于点E ， F ．
1. （1）【活动猜想】
  如图2，当点 $\text{[math]}$ 与点D重合时，四边形 $\text{[math]}$ 是哪种特殊的四边形？并说明理由．
2. （2）【问题解决】
  如图3，当 $\text{[math]}$ 与 $\text{[math]}$ 满足什么关系时，始终有 $\text{[math]}$ 与对角线 $\text{[math]}$ 平行？请说明理由．
3. （3）【深入探究】
  在（2）的情形下，设 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 分别交于点O ， P ，试探究三条线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间满足的等量关系，直接写出答案．
答案解析收藏纠错 + 选题