江西省宜春市高安市2023-2024学年七年级下学期数学期中...

更新时间：2024-05-16 浏览次数：25 类型：期中考试

一、选择题（本大题共6小题，每小题3分，共18分）

1. (2024七下·高安期中) 下列各数没有算术平方根的是（）

A . 0 B . 36 C . $\text{[math]}$ D . －10

答案解析收藏纠错 + 选题
2. (2024七下·高安期中) 下列各组数中，互为相反数的一组是（）

A . －2与 $\text{[math]}$ B . －2和 $\text{[math]}$ C . $\text{[math]}$ 与2 D . $\text{[math]}$ 和2

答案解析收藏纠错 + 选题
3. (2024七下·高安期中) 如图，小明用手盖住的点的坐标可能为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·高安期中) 如图，直线a、b被直线c所截， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
5. (2024七下·高安期中) 下列命题中，其中真命题的个数是（）
①平面直角坐标系内的点与有序实数对一一对应；
②内错角相等；
③如果两条直线都与第三条直线平行，那么这两条直线也互相平行；
④直线外一点到直线的距离是垂线段．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
6. (2024七下·高安期中) 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …，那么点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2024七下·仓山期末) 比较大小： $\text{[math]}$ 3．（“＞”“＜”或“=”）

答案解析收藏纠错 + 选题
8. (2024八下·邱县期末) 若电影院中“4排5号”记作 $\text{[math]}$ ，则 $\text{[math]}$ 表示的意义是．

答案解析收藏纠错 + 选题
9. (2024七下·高安期中) 如图，用直尺和三角尺作出直线AB、CD，得到AB∥CD的理由是．

答案解析收藏纠错 + 选题
10. (2024七下·高安期中) 已知点 $\text{[math]}$ 在第一象限，它到x轴的距离为3，到y轴的距离为6，则点P的坐标是．

答案解析收藏纠错 + 选题
11. (2024七下·高安期中) 把一张对边互相平行的纸条，按图折叠后，EF是折痕，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
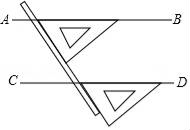
12. (2024七下·赣州期中) 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ ，且点E在直线 $\text{[math]}$ 的上方时，若这两块三角尺有两条边平行，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题6分，共30分）

13. (2024七下·高安期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2024七下·高安期中) 求下列各式中x的值．
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
15. (2024七下·高安期中) 已知 $\text{[math]}$ 的算术平方根是0， $\text{[math]}$ 的立方根是3，求 $\text{[math]}$ 的平方根．

答案解析收藏纠错 + 选题
16. (2024七下·高安期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ．说明 $\text{[math]}$ 的理由．

答案解析收藏纠错 + 选题
17. (2024七下·南昌期中) 在平面直角坐标系中，已知点 $\text{[math]}$ ，点 $\text{[math]}$ ．
1. （1）若M在x轴上，求m的值；
2. （2）若点M到x轴，y轴距离相等，求m的值；
3. （3）若 $\text{[math]}$ 轴，点M在点N的上方且 $\text{[math]}$ ，求n的值．
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共24分）

18. (2024七下·高安期中) $\text{[math]}$ 在平面直角坐标系中的位置如图所示，把 $\text{[math]}$ 向右平移5个单位，再向下平移4个单位，得到 $\text{[math]}$ ．
1. （1）请你在图上画出 $\text{[math]}$ ；
2. （2）直接写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的坐标；
3. （3）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2024七下·高安期中) 对于两个不相等的实数a ， b ，定义新的运算如下： $\text{[math]}$ ，如 $\text{[math]}$ ， $\text{[math]}$ ，如 $\text{[math]}$ ．
请你计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2024七下·高安期中) 已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A．
1. （1）求证：FE∥OC；
2. （2）若∠B=40°，∠1=60°，求∠OFE的度数．
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共18分）

21. (2024七下·高安期中) 如图， $\text{[math]}$ 交 $\text{[math]}$ 于E， $\text{[math]}$ ， $\text{[math]}$
1. （1）求证： $\text{[math]}$ ；
2. （2） M，N分别在 $\text{[math]}$ 、 $\text{[math]}$ 的延长线上， $\text{[math]}$ 和 $\text{[math]}$ 的平分线相交于F，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
22. (2024七下·高安期中) 对于平面直角坐标系 $\text{[math]}$ 中的不同两点 $\text{[math]}$ ， $\text{[math]}$ ，给出如下定义：若 $\text{[math]}$ ， $\text{[math]}$ ，则称点 $\text{[math]}$ ， $\text{[math]}$ 互为“倒数点”，例如：点 $\text{[math]}$ ， $\text{[math]}$ 互为“倒数点”．
1. （1）已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的“倒数点”点 $\text{[math]}$ 的坐标为；将线段 $\text{[math]}$ 向右平移2个单位得到线段 $\text{[math]}$ ，则线段 $\text{[math]}$ 上 $\text{[math]}$ 填“存在”或“不存在” $\text{[math]}$ “倒数点”．
2. （2）如图，在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，请判断该正方形的边上是否存在“倒数点”，并说明理由．
答案解析收藏纠错 + 选题

六、解答题（本大题12分）

23. (2024七下·高安期中) 如图，四边形OABC为长方形，以O为坐标原点，OC所在直线为x轴建立平面直角坐标系．已知点A的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ．
1. （1）直接写出点B的坐标为；
2. （2）有一动点D从原点O出发，以1个单位长度/秒的速度沿线段OA向终点A运动，当直线CD将长方形的周长分为 $\text{[math]}$ 两部分时，求D点的运动时间t值；
3. （3）在（2）的条件下，点E为坐标轴上一点，若三角形CDE的面积为15，求出点F的坐标．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

江西省宜春市高安市2023-2024学年七年级下学期数学期中...

副标题：

*注意事项：

江西省宜春市高安市2023-2024学年七年级下学期数学期中...

试题分析

总体分析

题量分析

难度分析

知识点分析