浙江省嘉兴市八校联盟2023-2024学年高二下学期数学期中...

更新时间：2024-06-18 浏览次数：9 类型：期中考试

一、选择题Ⅰ（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. (2024高二下·嘉兴期中) 函数 $\text{[math]}$ 的图象如图所示，它的导函数为 $\text{[math]}$ ，下列导数值排序正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高二下·嘉兴期中) 从6名同学中选出正、副组长各1名，不同的选法种数是（）

A . 30种 B . 11种 C . 15种 D . 35种

答案解析收藏纠错 + 选题
3. (2024高二下·嘉兴期中) $\text{[math]}$ 的展开式的第 $\text{[math]}$ 项的系数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二下·嘉兴期中) 设随机变量 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 2 B . 3 C . 6 D . 7

答案解析收藏纠错 + 选题
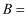
5. (2024高二下·嘉兴期中) 一个盒内有五个月饼，其中两个为果浆馅，三个为五仁馅，现从盒内随机取出两个月饼，若事件 $\text{[math]}$ “取到的两个月饼为同一种馅”， $\text{[math]}$ “取到的两个月饼都是五仁馅”，则概率 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二下·嘉兴期中) 甲､乙､丙等七人相约到电影院看电影《长津湖》，恰好买到了七张连号的电影票，若甲､乙两人必须相邻，且丙坐在七人的正中间，则不同的坐法的种数为（）

A . 240 B . 192 C . 96 D . 48

答案解析收藏纠错 + 选题
7. (2024高二下·嘉兴期中) 函数 $\text{[math]}$ 的图象如图所示， $\text{[math]}$ 为函数 $\text{[math]}$ 的导函数，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二下·嘉兴期中) 已知函数 $\text{[math]}$ ，若 $\text{[math]}$ ，其中 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题Ⅱ（本大题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分，有选错的得0分．）

9. (2024高二下·嘉兴期中) 设随机变量 $\text{[math]}$ 的分布列如表所示，则下列选项中正确的为（）
$\text{[math]}$
0
1
2
3
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高二下·嘉兴期中) 已知 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二下·嘉兴期中) 已知直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 相交于不同两点 $\text{[math]}$ ，曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线与在点 $\text{[math]}$ 处的切线相交于点 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（本大题共3小题，每小题5分，共15分）

12. (2024高二下·嘉兴期中) 函数 $\text{[math]}$ 的导函数是.

答案解析收藏纠错 + 选题
13. (2024高二下·嘉兴期中) 某区学生参加模拟大联考，假如联考的数学成绩服从正态分布，其总体密度函数为： $\text{[math]}$ ，且 $\text{[math]}$ ，若参加此次联考的学生共有 $\text{[math]}$ 人，则数学成绩超过 $\text{[math]}$ 分的人数大约为．

答案解析收藏纠错 + 选题
14. (2024高二下·嘉兴期中) 用 $\text{[math]}$ 这九个正整数组成无重复数字且任意相邻的三个数字之和是 $\text{[math]}$ 的倍数的九位数，这样的九位数有个（用数学作答）

答案解析收藏纠错 + 选题

四、解答题（本大题共5小题，共77分，解答应写出文字说明、证明过程或演算步骤．）

15. (2024高二下·江油月考) 已知函数 $\text{[math]}$ .
1. （1）求曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程；
2. （2）求 $\text{[math]}$ 的极值.
答案解析收藏纠错 + 选题
16. (2024高二下·嘉兴期中) 已知 $\text{[math]}$ 的展开式中，所有项的系数之和是512．
1. （1）求展开式中含 $\text{[math]}$ 项的系数；
2. （2）求 $\text{[math]}$ 的展开式中的常数项.
答案解析收藏纠错 + 选题
17. (2024高二下·嘉兴期中) 为落实“坚持五育并举，全面发展素质教育，强化体育锻炼”的精神，某高中学校鼓励学生自发组织各项体育比赛活动．甲、乙两名同学利用课余时间进行乒乓球比赛．规定：每局比赛中获胜方记1分，失败方记0分，没有平局．首先获得5分者获胜，比赛结束．假设每局比赛甲获胜的概率都是 $\text{[math]}$ ．
1. （1）求比赛结束时恰好打了6局甲获胜的概率；
2. （2）若甲以 $\text{[math]}$ 的比分领先，记X表示到结束比赛时还需要比赛的局数，求X的分布列．
答案解析收藏纠错 + 选题
18. (2024高二下·嘉兴期中) 甲箱的产品中有5个正品和3个次品，乙箱的产品有4个正品和3个次品．
1. （1）从甲箱中任取2个产品，求这2个产品都是次品的概率；
2. （2）如果依次不放回地从乙箱中抽取2个产品，每次取1个，已知第二个是次品的条件下，求第一个是正品的概率；
3. （3）若先从甲箱中任取2个产品放入乙箱中，再从乙箱中任取一个产品，求取出这个产品是正品的概率．
答案解析收藏纠错 + 选题
19. (2024高二下·嘉兴期中) 已知函数 $\text{[math]}$
1. （1） $\text{[math]}$ 是 $\text{[math]}$ 的极值点， $\text{[math]}$ 有两个零点，求 $\text{[math]}$ 的取值范围；
2. （2）令 $\text{[math]}$ ，讨论 $\text{[math]}$ 的单调性；
3. （3）当 $\text{[math]}$ 时，设 $\text{[math]}$ 和 $\text{[math]}$ 为两个不相等正数，且 $\text{[math]}$ ，证明： $\text{[math]}$ ．
答案解析收藏纠错 + 选题