一、选择题(本大题共6个小题,每小题3分,共18分)
-
-
-
-
4.
(2024·九江模拟)
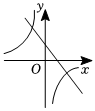
已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )
-
二、填空题(本大题共6个小题,每小题3分,共18分)
-
-
-
-
9.
(2024·九江模拟)
《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的

).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点
A ,
B ,

在同一水平线上,

和

均为直角,

与

相交于点

. 测得

, 则树高

m.

-
10.
(2024·九江模拟)
如图,

为等边

的

边的中点,点

是

上的一个动点,连接

, 将

沿

翻折,得到

, 连接

, 若

, 则

的度数为
.

-
11.
(2024·九江模拟)
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为
.

三、解答题(本大题共5个小题,每小题6分,共30分.)
-
-
(1)
计算:

-
(2)
解分式方程:

.
-
-
14.
(2024·九江模拟)
在

中,

,

,

、

分别为边

、

的中点.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).

-
(1)
在图1中画一个以点

、点

为顶点的菱形;
-
(2)
在图2中画一个以点

、点

为顶点的矩形.
-
15.
(2024·九江模拟)
先化简,再求值,其中
x是满足条件

的合适的非负整数.以下是某同学化简分

的部分运算过程:
-
-
-
16.
(2024九上·清远期末)
甲骨文是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,小明在了解了甲骨文后,制作了如图所示的四张卡片

这四张卡片分别用字母

,

,

,

表示,正面文字依次是文、明、自、由,这四张卡片除正面内容不同外,其余均相同

, 现将四张卡片背面朝上,洗匀放好.

-
(1)
小明从中随机抽取一张卡片,抽取卡片上的文字是“文”的概率为.
-
(2)
小明从中随机抽取一张卡片不放回,小亮再从中随机抽取一张卡片,请用列表法或画树状图法计算两人抽取的卡片恰好组成“文明”一词的概率.
四、解答题(本大题共3个小题,每小题8分,共24分.)
-
17.
(2024·九江模拟)
已知

是双曲线

上的一点,
B点是双曲线

上的一点,
B点的横坐标为

,

轴,且
P是
x轴负半轴上的一点;
-
(1)
求

的函数关系式;
-
(2)

的面积是
;
-
(3)
若

是等腰三角形,直接写出
P的坐标.
-
18.
(2024·九江模拟)
如图①,某款线上教学设备由底座,支撑臂

, 连杆

, 悬臂

和安装在
D处的摄像头组成.如图②是该款设备放置在水平桌面
l上的示意图.已知支撑臂

,

,

, 固定

, 可通过调试悬臂

与连杆

的夹角提高拍摄效果.

-
-
(2)
已知摄像头点
D到桌面
l的距离为

时拍摄效果较好,那么此时悬臂

与连杆

的夹角

的度数约为多少?(参考数据:

)
-
19.
(2024·九江模拟)
如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且

=

,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.

-
-
(2)
若AG=6,GE=6

,求⊙O的半径.
五、解答题(本大题共2个小题,每小题9分,共18分.)
-
20.
(2024·九江模拟)
为了进一步了解某校八年级学生的身体素质情况,体育老师抽测了该校八年级(1)班50名学生一分钟的跳绳次数,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:请结合图表完成下列问题:
组别 | 次数 | 频数(人数) |
第1组 | 
| 6 |
第2组 | 
| 8 |
第3组 | 
| 
|
第4组 | 
| 18 |
第5组 | 
| 6 |

-
(1)
本次调查为(填全面调查或抽样调查),样本容量为;
-
(2)
 ▲
▲ ;并把频数分布直方图补充完整;
-
(3)
若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?
-
21.
(2024·九江模拟)
定义:若两条抛物线的顶点关于原点对称,二次函数的二次项系数互为负倒数,这样的两条抛物线称之为“共生抛物线”,如抛物线

与

是共生抛物线,已知抛物线

的顶点是点
P , 它的共生抛物线

的顶点是
Q;

-
(1)
点
P的坐标是
, 点
Q的坐标是
,抛物线

的函数关系式是
.
-
(2)
直线

与抛物线

、

均有两个交点,这些交点从左到右分别是
A、
B、
C、
D .
①求m的取值范围 ▲ ;
②若 , 求m的值;
, 求m的值;
六、解答题(本大题共12分.解答应写出文字说明,证明过程或演算步骤)
 B .
B .  C .
C .  D .
D . 
 B .
B . 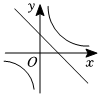 C .
C . 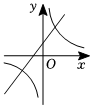 D .
D . 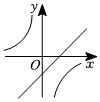






, 求m的值;
的对角线相交于点
, 点
又是正方形
的一个顶点,而且这两个正方形的边长相等,无论正方形
绕点
怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的
.想一想,这是为什么?(此问题不需要作答)
的对角线相交于点
, 点
落在线段
上,
(
为常数).

的直角顶点
与点
重合,两直角边分别与边
,
相交于点
,
.
▲ ;
. (提示:借鉴解决【问题背景】的思路和方法,可直接证明
;也可过点
分别作
,
的垂线构造全等三角形证明.请选择其中一种方法解答问题②.)
沿
方向平移,判断
与
的数量关系(用含
的式子表示),并说明理由.
在边
上,
, 延长
交边
于点
, 若
, 求
的值.